Trygonometria
Justa: Narysuj wykres funkcji f w podanym przedziale:
a)f(x)=2cosx*|sinx|,
x∊<0;2π>
b) f(x)=2sinx−
√1−cos2x,
x∊<π;2π>
| | 1 | | 1 | |
c) f(x)=sin2x*√ |
| + |
| |
| | sin2x | | cos2x | |
| | π | | 3π | |
x∊(0;2π)\{ |
| , π, |
| } |
| | 2 | | 2 | |
25 lut 20:03
Justa: najbardziej zależy mi na podpunkcie a)
bo b) i c) wiem mniej wiecej jak zrobić

25 lut 20:06
Aga1.: f(x)=2cosxsinx=sin2x, gdy sinx≥0
f(x)=−2cosxsinx=−sin2x, gdy sinx<0
25 lut 20:08
Marcin:
Dla sinx≥0 masz
2cosxsinx,
Dla sinx<0 masz:
−2cosxsinx
25 lut 20:08
Mila:
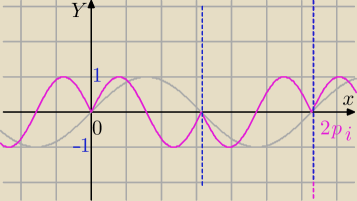
1)
|sinx|=sinx dla x∊<0,π> wtedy masz wzór funkcji:
f(x)=2cosx sinx⇔f(x)=sin(2x)
2)
|sinx|=−sinx dla x∊(π,2π> wtedy masz wzór funkcji:
f(x)=−2cosx sinx⇔f(x)=−sin(2x)
25 lut 20:14
Justa: skąd to f(x)=−2cosxsinx=−sin2x −>>> skąd ten wynik,jakie przekształcenia trzeba zrobić, aby
dojść to tego rozwiazania.

25 lut 20:14
Mila:
wzór :
sin(2α)=2sinα cosα
25 lut 20:31
Justa: dziękuję

25 lut 20:52
Justa: a pomoże ktoś jednak z tym c)
udało mi się przekształcić to do tego momentu:
| | 1 | |
sin2x*| |
| | i co dalej ? |
| | sinx*cosx | |
25 lut 21:15
Mila:
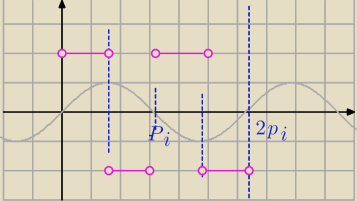
| | 2 | |
f(x)=sin(2x)*| |
| | |
| | sin(2x) | |
1)
| | π | | 3π | |
|sin(2x)|=sin(2x)⇔x∊(0, |
| )U <π, |
| ) |
| | 2 | | 2 | |
wtedy masz wzór funkcji:
| | 2 | |
f(x)=sin(2x)* |
| ⇔f(x)=2 |
| | sin(2x) | |
2)
| | π | | 3π | |
|sin(2x)|=−sin(2x)⇔x∊( |
| ,π)U <( |
| ,2π) |
| | 2 | | 2 | |
wtedy masz wzór funkcji:
| | 2 | |
f(x)=sin(2x)* |
| ⇔f(x)=−2 |
| | −sin(2x) | |
25 lut 21:33

 1)
|sinx|=sinx dla x∊<0,π> wtedy masz wzór funkcji:
f(x)=2cosx sinx⇔f(x)=sin(2x)
2)
|sinx|=−sinx dla x∊(π,2π> wtedy masz wzór funkcji:
f(x)=−2cosx sinx⇔f(x)=−sin(2x)
1)
|sinx|=sinx dla x∊<0,π> wtedy masz wzór funkcji:
f(x)=2cosx sinx⇔f(x)=sin(2x)
2)
|sinx|=−sinx dla x∊(π,2π> wtedy masz wzór funkcji:
f(x)=−2cosx sinx⇔f(x)=−sin(2x)


