nierówność z wartością bezwzględną formerangel: Rozwiąż nierówność : ||x + 1| − x| ≤ 2 Czy mniej więcej tak to powinno wyglądać ? Co z drugim przypadkiem bo nie wiem co z nim zrobić odrzuciłbym go bo tam jest ≤ a wartość nie może być równa −2 czekam na wasze zdanie |x +1| − x ≤ 2 v |x +1| − x ≥ −2 1) x∊(−∞, −1) −x − 1 −x ≤ 2 x ≥ −³₂ 2) x∊ <−1, ∞) x +1 − x ≤ 2 0 ≤ 1 więc: x ∊ <−³₂, −1)u<−1, +∞) = <−³₂, +∞)

Ajtek: Robisz analogicznie

formerangel: sorki, tam (czyli" bo tam jest ... ) powinno być ≥ a nie ≤

formerangel: ok, jak wyjdzie mi tak jak w opdowiedziach, dam znać

formerangel: |x +1| − x ≤ 2 część wspólna z dwóch przypadków <−³₂, +∞) |x +1| − x ≥ −2 część wspólna z dwóch przypadków x = R czyli co ? x∊R u <−³₂, +∞) = R ? a z tyłu mam samo <−³₂, +∞)

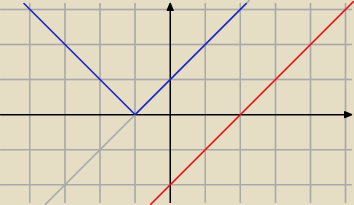
Aga1.: Druga graficznie Ix+1I≥x−2 dla x∊R

Aga1.: Powinieneś użyć spójnika i . Wyjdzie tak jak w książce.

mathnull: aaaa