Planimetria cd bezendu: W trapez prostokątny można wpisać okrąg. Jedna z jego podstaw ma długość a , druga jest trzy razy dłuższa. Oblicz pole trapezu oraz długość odcinka łączącego środki ramion trapezu Odcinek łączący środki ramion ma 2a, jak wyliczyć h, 4a=AD+CB

Eta:

	1
Z warunku wpisania okręgu w trapez: h+c=4a ⇒ c= 4a−h , h∊(0,		a)
	4

i z tw. Pitagorasa w trójkącie BEC h=......

bezendu:

	1
Dziękuję ślicznie Tylko czemu h∊(0,		a) ?
	4

Eta: c=4a−h , c>0 ⇒ 4a−h>0 h< 4a ⇒h∊(0, 4a) ( tak ma być .... sory za zły wpis

bezendu: OK.

bezendu: Środek okręgu wpisanego w trapez prostokątny, znajduje się w odległości 4 oraz 8 od końców dłuższego ramienia trapezu. Oblicz pole tego trapezu Hmm ? wskazówkę proszę

Mila: Rysunek nie koresponduje z danymi.

zawodus: Od ramienia

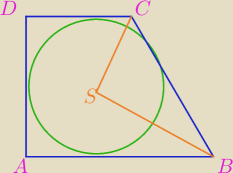
bezendu: Ja przeczytałem podstawy.

zawodus: Liczysz Wysokość tego trójkąta z wierzchołka S. Czym ten odcinek jest dla okręgu?

bezendu: ?

zawodus: Ten trójkąt jest prostokątny. Dlaczego?

Mila: Promień jest prostopadły do ramienia w punkcie styczności, to jest wysokością opuszczoną na BC. Już Ci wcześniej wyjaśniane było, że ΔBSC jest prostokątny Możesz obliczyć |BC|, potem pole Δ na dwa sposoby.

bezendu: Wcześniej ? Ale punkt C nie jest punktem styczności.

zawodus: ale Wysokość trójkąta z punktu S jest.

zawodus: W ciągu ostatniego tygodnia było podobne zadanie.

Eta: (x+y)²= 80 ⇒ x+y=.......

	4*8
r=		=......
	x+y

P(tr)= 2r²+ P(tr FBCG) = .....

bezendu: To, że w trójkątach CSE oraz BSE są kąty proste to pewne ale CSB ?

Eta: Środek okręgu wpisanego znajduje się w punkcie przecięcia dwusiecznych kątów i 2α+2β= 180^o ⇒ α+β= 90^o= |<BSC|

Mila: Środek okręgu wpisanego w wielokąt leży na przecięciu dwusiecznych kątów .Eta zaznaczyła odpowiednio. 2α+2β=180 suma kątów przy ramieniu trapezu α+β=90⇔∡CSB=90 z sumy katów w Δ

Eta:

bezendu: Dziękuję, już zrozumiałem.

Eta: "zrozumiałeś" −−−− teraz zapamiętaj tę własność!

bezendu: Są jeszcze jakieś własności odnośnie trapezu prostokątnego ?

bezendu: Pole trapezu prostokątnego opisanego na okręgu jest równe 5, a obwód trapezu wynosi 10. Oblicz długość promienia okręgu r=1 tak ?

zawodus: Jak Dobrze podstawiłeś do wzoru to tak

Eta: Napisz jak rozwiązywałeś .... jestem ciekawa

bezendu: obwód wynosi 10 więc a+b+c+d=10 a+b=5

a+b
	*h=5
2

h=2

	h
r=
	2

r=1 Gorszy jest trapez równoramienny brrr...

Mila: P=p*r, gdzie p− połowa obwodu p=10:2=5 5=5*r⇔r=1

bezendu: Czy w trapezie równoramiennym przekątna zawsze zawiera się w dwusiecznej kątów ?

Eta: Ooo .. Mila już napisała

Eta:

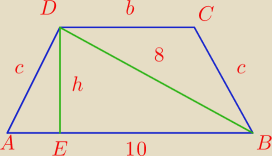
bezendu: Mam trapez równoramienny którego dłuższa podstawa ma długość 10 a przekątna ma długość 8 obliczyć pole trapezu Wskazówka, nie prawie gotowiec... !

zawodus: To zadanie ma za mało danych

wredulus_pospolitus: to są trzy z całej rodziny trapezów równoramiennych spełniających podane przez Ciebie warunki, jak widzisz ... zbyt mało danych ... konieczne by było otrzymać jeszcze jakiś kąt, jakaś proporcja, cokolwiek.

bezendu: Tyle jest danych tylko, zadanie z pazdro

wredulus_pospolitus: musi coś jeszcze być ... jakakolwiek dodatkowa informacja ... czyli coś na czym można oprzeć wybór konkretnego czworokąta z rodziny zaprezentowanej o 9:08

zawodus: Zobacz jeszcze raz Jak nie to zadanie źle ułożone

bezendu: Sprawdzałem, dobrze przepisałem

Mila: Nie jest wpisany w okrąg?

Piotr 10: bezendu to zadanie ze zbioru zadań z Pazdro ( taki czerwony) ?

bezendu: Nie, nie ma nic w treści o okręgu. Skoro nie da się policzyć to biorę się za inne zadania.