Idiota Hejo: Następne zadanie ... Wyznacz wszystkie wartości parametrów p i q, dla których nierówność (18 − 3x − x²)(x² + px − 2qx + 6q) ≤ 0 jest spełniona przez każdą liczbę rzeczywistą.

J: Aby ta nierówność była prawdziwa dla każdego x ∊ R, obydwa trójmiany muszą miec te same miejsca zerowe. Ponieważ pierwszy ma miejsca zerowe x₁ = − 6 oraz x₂ = 3, więc musi być: (−6)² −6(p−2q) + 6q = 0 oraz 3² +3(p−2q) + 6q = 0 Z powyższego układu równań oblicz p i q

Domel: lub z zależności: a*b ≤ 0 => (a ≥ 0 ∧ b ≤ 0) ∨ (a ≤ 0 ∧ b ≥ 0)

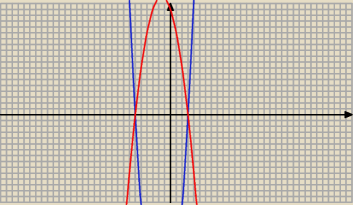
Domel: Z której właśnie dochodzimy do wspólnych pierwiastków − to informacyjnie − gdybyś się zastanawiał "a dlaczego wspólne pierwiastki Na czerwono − pierwsza funkcja kwadratowa a na niebiesko − druga − mają wspólne miejsca zerowe więc ich wymnożenie na pewno będzie ≤ 0