 w kulę o promieniu 3 wpisano cztery jednakowe kule tak,że środki wszystkich kul leżą w jednej
płaszczyźnie i każda z małych kul jest styczna do dwóch małych kul i dużej. Oblicz objętość
małej kuli.
w kulę o promieniu 3 wpisano cztery jednakowe kule tak,że środki wszystkich kul leżą w jednej
płaszczyźnie i każda z małych kul jest styczna do dwóch małych kul i dużej. Oblicz objętość
małej kuli.
 Skoro leżą w jednej płaszczyźnie, to problem sprowadza się do czterech okręgów wpisanych w
jeden duży.
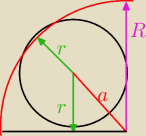
Zauważ, że promień dużego okręgu, to odcinek zielony plus fioletowy.
Odcinek zielony, to promień małego okręgu, a odcinek fioletowy, to przekątna kwadratu o boku
równym promieniowi małego okręgu.
Skoro leżą w jednej płaszczyźnie, to problem sprowadza się do czterech okręgów wpisanych w
jeden duży.
Zauważ, że promień dużego okręgu, to odcinek zielony plus fioletowy.
Odcinek zielony, to promień małego okręgu, a odcinek fioletowy, to przekątna kwadratu o boku
równym promieniowi małego okręgu.
 To taki rysunek poglądowy na płaszczyźnie środków kul (nie patrz na niedociągnięcia i brak
styczności na rysunku − te kule
To taki rysunek poglądowy na płaszczyźnie środków kul (nie patrz na niedociągnięcia i brak
styczności na rysunku − te kule  SĄ STYCZNE)
Masz promień dużej czerwonej kuli − czy możesz wyznaczyć promień którejś z małych kul?
SĄ STYCZNE)
Masz promień dużej czerwonej kuli − czy możesz wyznaczyć promień którejś z małych kul?
| r | √2 | ||
= sin45° = | |||
| a | 2 |
| r | √2 | ||
= | |||
| R−r | 2 |
| √2 | ||
r = | (R−r) | |
| 2 |