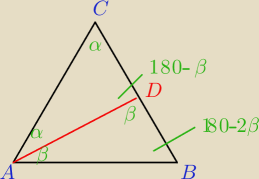
Ostatnia próba bezendu: Punkt D leży na boku BC trójkąta równoramiennego, w którym |AC | = |BC | . Odcinek AD dzieli trójkąt ABC na dwa trójkąty równoramienne takie, że |AD | = |CD | i |AB | = |BD | . Wykaż, że |∡ADC | = 5|∡ACD | . α+β=180−2β α=180−3β 180−3β+180−3β+180−β=180 7β=360

	360
β=
	7

	360
α=180−3*
	7

	180
α=
	7

	900
∡ADC=
	7

	180
∡ACD=
	7

C.N.W ?

Eta: Może być, ale takie to "pokrętne" Suma kątów w trójkącie ABC : 7α=180^o to |<ADC|= 180^o−2α= 7α−2α= 5α i otrzymujesz tezę

bezendu: Robię tak jak potrafię. Czyli taki dowód byłby uznany ?

bezendu: I to mnie cieszy, dziękuję.

Mila: Może być , ale trzeba pisać w którym Δ liczysz sumę kątów.

bezendu: To mam napisać, że liczę kąty w ΔADC ?

Mila: Piszesz : w ΔADC: ...

Trivial: Jeśli chcesz żeby ktoś szybko sprawdził, to pisz z których trójkątów biorą się równania. Sam musiałem nieźle pokombinować, żeby zobaczyć skąd te równania się biorą.

Trivial: A poza tym Twój rysunek jest strasznie mylący.

Eta: No tak.... jeszcze zapomniałam dopisać: rysunek do kitu"!

Eta: Mam nadzieję,że takiego rysunku nie namalujesz na maturze?

bezendu: Na maturze namaluję piękny rysunek

Eta:

bezendu: Oczywiście jak będę umiał zrobić zadanie.

bezendu: Podstawa trójkąta równoramiennego i środkowe poprowadzone z jej konców mają długość a . Oblicz długość wysokości poprowadzonej do podstawy od czego zacząć, ''nie dokończ'' tylko wskazówka !

oskar: Np. dwa razy twierdzenie cosinusów, a później Pitagoras.

bezendu: Chyba nie..

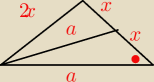
oskar: kropa to α

oskar: to /\ dwa razy cosinusów dla małego i dużego trójkąta a później pitek jak opuscisz wysokosc na a.

Mila: Środkowe Δ przecinają się w jednym punkcie i dzielą w stosunku 2:1 licząc od wierzchołka. Ta wysokość też jest środkową.

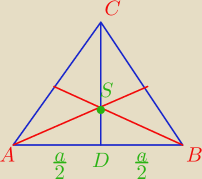
bezendu: Trójkąt ASB jest podobny do ABC ?

oskar: z jakiej cechy niby?

zawodus: z jakiej cechy?

zawodus: z jakiej cechy?

bezendu: Czyli to raczej niewypał...

Mila: Przeczytaj co napisałam 21:06.

	2
|AS|=		a itd, to wszystko.
	3

zawodus: Z Jakiej cechy?

zawodus: Z Jakiej cechy?

bezendu:

	√7a
To wychodzi		?
	2

oskar: Tak

zawodus: Ten internet jest do kitu Mila proszę o usunięcie tych wszystkich moich postów

Mila: Dobrze.

Mila: Dlaczego Zawodus, to jest w tym zadaniu dobre pytanie. Podobieństwo jest, ale nie w tym Δ co napisał bezendu.

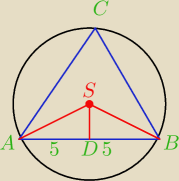
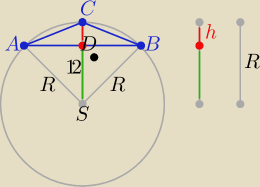
bezendu: W okrąg o promieniu 13 wpisano rozwartokątny trójkąt równoramienny o podstawie 10. Oblicz pole tego trójkąta SD=12

Mila: Źle rysunek. Gdzie leży środek okręgu opisanego na trójkącie rozwartokątnym? Weź linijkę, cyrkiel i opisz okrąg na Δ rozwartokątnym. WAŻNE

Eta:

bezendu: Na przecięciu symetralnych

Mila: Dobrze, W Δ prostokątnym w środku przewiprostokątnej w Δ ostrokątnym .... w Δ rozwartokątnym...

bezendu: w rozwartokątnym to środek jest poza trójkątem.

Mila: No i teraz rozwiązuj i daj odp.

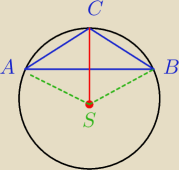
bezendu: Ale jak mam policzyć wysokość w tym trójkącie ?

Mila: |SB|=13 |SC|=13 |AO|=|OB|=5 Pitagoras się kłania.

Eta: h=13−12=1 ( nie osłabiaj mnie

bezendu: A no tak SB to też promień.

Radek: W trójkącie ABC dane są długości boków |AB | = 20 cm ,|AC | = |BC | = 26 cm . Wyznacz długość środkowej BD . Mogę korzystać z tego pięknego wzoru na długość środkowej ? d=0,5√2a²+2b²−c² c−bok na który opuszczona jest wysokość ? d=3√41

Radek: Przepraszam, że tu ale skoro planimetria to i ja chcę się nuaczyć.

bezendu: A tak trudno założyć swój temat

bezendu: W trójkącie równoramiennym podstawa AB ma długość 8cm. Promień okręgu, stycznego w punktach A i B do prostych zawierających ramiona AC i BC trójkąta, ma długość 5cm. Oblicz pole trójkąta ABC Proszę o rysunek

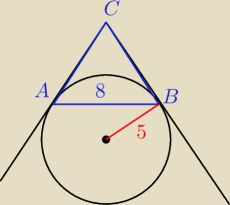
Saizou : proszę ....

bezendu: Tutaj trzeba z podobieństwa ?

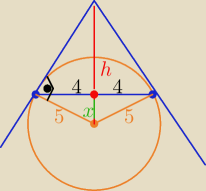
Eta: x=..... i 4²=x*h ⇒h=.....

bezendu: Eta ja pisałem, że chcę tylko rysunek a nie ''prawie gotowca'' którego mam tylko dokończyć....

Eta: Więcej już z Tobą nie gadam

bezendu: Nie obrażaj się, tylko nie pisz mi prawie gotowców, bo ja nigdy takowych nie chciałem i nie chcę, wolę wskazówkę do samodzielnego rozwiązania, niż wszystko rozpisane a jedyna moja trudność to podstawić liczby.

bezendu:

	64
Pole wyszło		cm2
	3

Saizou :

bezendu: Ramię trójkąta równoramiennego jest dwa razy dłuższe od podstawy. Wyznacz obwód trójkąta, jeśli środkowa poprowadzona do ramienia ma długość d

d		a
	=		?
sin(180−2α)		sinα

Saizou : policz i zobaczysz że zostanie ci cosα

bezendu: dsinα=asin2α

	dsinα
a=
	2sinαcosαa

	d
a=
	cosα

Obw=5a

	5d
Obw=
	cosα

Coś chyba nie tak poszło...

Saizou : ale nie masz danego kąta, tylko d

Mila: H cosA tw. cosinusów⇒a

bezendu: Czemu trzeba obliczać H ?

Saizou : i....

Mila: A nie trzeba, tylko narysować, aby mieć Δ prostokątny.

bezendu: Nie mogę tutaj nic z kątami ?

Saizou : nie, pośredni możesz wykorzystać ale w wyniku ma być samo d

bezendu:

	5√6a
z pitagorsa tak jak radzi Mila mam obwód
	3

Mila: Raczej nie korzystałabym, tu masz wiele innych możliwośći. Gdy narysujesz wysokość opuszczoną na bok a, to ona jest środkową, dzieli się ze środkową d w stosunku 2:1. Pitagoras dwa razy. albo tak jak wcześniej podałam, najprościej.

	1   a 2
cos A=		i tw. cosinusów w dolnym Δ.
	2a

Mila: Dobrze.

bezendu: Dziękuję, to nie są raczej zadania na maturę ale cóż.

Mila: Dlaczego nie są?

bezendu: W arkuszach widuję o wiele trudniejsze od tych, jest wymieszane podobieństwo, tw sinusów i cosinusów, bo na poziomie R sprawdzają znajomość tych twierdzeń.

Mila: Najpierw proste zastosowania i powinieneś jednak rozwiązywać zadanie różnymi sposobami, bo wtedy utrwalasz zastosowanie różnych twierdzeń. Potem będziesz miał w głowie zanotowne różne strategie.

bezendu: Dobrze jutro rozwiąże więcej zadań.

zombi: Do tych zadań jak poprzednie przydaje się tw. Stewarta, tzn. żeby nie używać po 2 razy twierdzenia cosinusów to możemy zastosować gotowy wzorek i podać się na to twierdzenie. http://en.wikipedia.org/wiki/Stewart%27s_theorem Taki offtopic, może się komuś przyda

zawodus: przydaje się tylko trzeba je pamiętać A ja mam zwyczaj, że jak czegoś długo nie używam to zapominam