zad optymalizacyjne AK: Boki trójkąta prostokątnego ABC mają długości |AC| = 3, |BC| = 4, |AB| = 5 Prosta L, równoległa do prostej AB przecina bok AC i BC odpowiednio w punktach M i N. S oznacza środek odcinka AB oraz |MC| = x. Pole P(x) trójkąta MNS jest funkcją zmiennej x. Znajdź wzór tej funkcji Zbadaj jaką największą wartość moze przyjmowac pole trojkata MNS to zadanie jest w paru miejscach w internecie ale zadne rozwiazanie nie jest dla mnie jasne prosze o pomoc

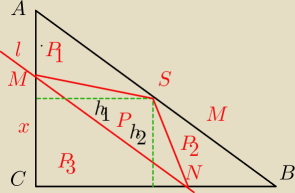
Janek191: Mamy I AC I = 3 , I BC I = 4 , I AB I = 5, I MC I = x l II pr AB

	3		x		4
oraz		=		⇒ I CN I =		x
	4		I CN I		3

P₁ − pole Δ AMS P₂ − pole Δ NBS P₃ − pole Δ MCN P − pole Δ MNS h₁ = 0,5*4 = 2 h₂ = 0,5*3 = 1,5 więc P = 0,5*3*4 − ( P₁ + P₂ + P₃)

	4		4
P(x) = 6 − [ 0,5*( 3 − x)*2 + 0,5*( 4 −		x)*1,5 + 0,5* x*		x]
	3		3

	2
P( x) = 6 − [( 3 − x ) + ( 3 − x) + (		x2) ]
	3

	2
P( x) = 6 − [ 6 − 2x +		x2]
	3

	2
P( x) = 2x −		x2
	3

lub

	2
P(x) = −		x2 + 2x
	3

	2
a = −		< 0
	3

	− 2
więc funkcja P przyjmuje największą wartość dla x = p =		=1,5
	−43

czyli

	2		3		3
Pmax = −		*(		)2 + 2*		= 1,5
	3		2		2

===========================

Janek191: Literka M między B i S jest niepotrzebna

AK: dzięki max