Zadanie Ewelina: Bardzo proszę o pomoc w rozwiązaniu zadania! Dane jest przekształcenie płaszczyzny P określone wzorem : P(x,y) = (−x,y+1), gdzie x,y∊R A)znajdź równanie obrazu okręgu o: x²+y²−2y−4=0 oraz wyznacz równania osi symetrii figury, która jest sumą okręgu o i jego obrazu w przekształceniu P.

Ewelina: nie proszę o rozwiązanie, lecz o naprowadzenie chociażby.

Zbronek: O_o: (−x)²+(y+1)²−2(y+1)−4=0 r−nia osi symetrii to r−nie prostej łączącej środki okręgów i r−nie prostej która jest symetralną od odcinka łączącego środki okregów

Ewelina: nie rozumiem?

Ewelina: proszę o pomoc

Ewelina: ponawiam prośbę, bardzo mi zależy na rozwiązaniu tego zadania

Zbronek: Przekształcenie P(x,y)=(−x,y+1) czyli x "zamienia" na −x ,a y na y+1.Tak otrzymasz r−nie obrazu okręgu.Wykonaj działania O_o i napisz jak wygląda r−nie obrazu

Zbronek: O_o: x²+y²+2y+1−2y−2−4=0 O_o: x²+y²−5=0 r−nie obrazu

Zbronek: (x−a)²+(y−b)²=r² to jest równanie okręgu o śr.S(a,b) i promieniu r nasze okręgi ,jeśli zapiszemy je w tej postaci to : O:(x−0)²+y²−2y+1−1−4=0 ⇒ (x−0)²+(y−1)²=√5² ⇒ S(0;1) O_o: (x−0)²+(y−0)²=√5² ⇒ S(0;0)

Zbronek: Teraz napisz r−nie prostej przechodzącej przez te dwa pkty−to będzie jedna z szukanych osi symetrii

Zbronek: ta prosta to x=0 czyli oś OY

Zbronek: druga oś symetrii przechodzi przez środek odcinka łączącego środki,czyli przez pkt (0,1/2) napisz r−nie prostej przechodzącej przez ten pkt i prostopadłej do OY

Zbronek:

	1
y=		druga oś symetrii
	2

Zbronek: this is the end

Ewelina: niestety żaden wynik nie zgadza się z odpowiedziami. Nie mam pojęcia co tu zrobiłeś szczerze mówiąc

Ewelina: niestety żaden wynik nie zgadza się z odpowiedziami. Nie mam pojęcia co tu zrobiłeś szczerze mówiąc

Zbronek: w/g mnie to tak ma być,ale mogę się mylić.

Bogdan: Podbijam, zaraz sprawdzę

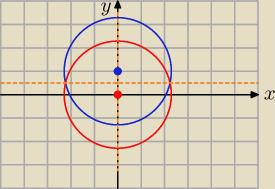
Bogdan: x² + y² − 2y − 4 = 0, środek S = (0, 1), promień R = √1² + 0² + 4 = √5 x' = −x, y' = y + 1 Obraz: (x')² + (y')² − 2y' − 4 = 0 ⇒ (−x)² + (y + 1)² − 2(y + 1) − 4 = 0 ⇒ ⇒ x² + y² − 5 = 0, środek S' = (0, 0), promień R' = √5 Są dwie osie symetrii. Pierwsza jest prostą przechodzącą przez środki okręgów, jest to prosta x = 0 (oś y). Drugą wyznaczamy odejmując równania okręgów stronami: (x² + y² − 2y − 4) − (x² + y² − 5) = 0

	1
−2y + 1 = 0 ⇒ y =
	2

Witaj Zbronku. Twoje rozwiązanie jest prawidłowe. Podobnie jak Tim, obserwuję Twoje wpisy na forum i z przyjemnością stwierdzam, że są rzeczowe i pomagające w zrozumieniu prezentowanego przez Ciebie zagadnienia, a także, że unikasz podawania gotowych rozwiązań. Widać fachową głowę. Pozdrawiam

tim: Nie ma tak , jestem lepszy..

tim: Oczywiście żartuje

Zbronek: Dzięki Bogdanie,ulżyło mi.To jest tak,że przyjmuje się ,że odp. w podręcznikach są prawidłowe(nie bez racji,bo tak powinno być).Jeśli kilka osób powie(czyt.:"jeśli w Książce jest napisane") ,że jesteś koniem, to kup sobie siodło.

Zbronek: myślę ,że relatywnie to "tim"−ie jesteś lepszy.

tim: Chyba tylko od osła ...

tim: Dla jasności: chodzi o zwierze

Igor: znajdź równanie prostej łączącej środek okręgu o równaniach: x²+y²−6x+8y=0 x²+y²+2x−12y+1=0 /3 x²+y²−6x+8y=0 x²+y²+6x−36y+3=0 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− −28y+3=0 −28y=3 / : (−28)

	3
y=
	−28

i co dalej

PW: To mnożenie stronami przez 3 wykonałeś źle. Chyba lepiej nie szukać punktów wspólnych tych dwóch okręgów, ale znaleźć ich środki (rozwiązując układ równań znajdziesz punkty leżące na osi symetrii prostopadłej do prostej łączącej środki, a więc utrudniasz sobie dojście do celu; zresztą gdyby okręgi nie miały punktów wspólnych, to w ogóle jest nieskuteczne).

Bartek: Wszyscy to zadanie rozwiązali źle

Bartek: Równanie okręgu x²+y²−2y−4=o przekształcamy do tzw. postaci kanonicznej x²+(y−1)²=5. Okrąg ten ma środek S(0,1) i promień r=√5. W podanej izometrii będzie miał postać x²+(y−2)²=5

Mila: 1) Dany okrąg: x²+(y−1)²=5 Przekształcenie jest izometrią, można to wykazać lub zauważyć, że jest złożeniem symetrii względem OY i translacji zatem jest izometrią. wtedy : r'=r=√5 S=(0,1) S'=(0,2) II sposób ( nie sprawdzamy, czy jest izometrią, korzystamy z wzorów) x'=−x y'=y+1 stąd: x=−x' y=y'−1 po podstawieniu do równania okręgu mamy: x'²+(y'−1−1)²=5⇔ x²+(y−2)²=5 ==========

Eta: Hej Mila Bartek "wykopał" zadanie z 2009 r