Pole czworokąta. nokia: Dany jest kwadrat ABCD o boku długości 2. Niech E, F będą środkami boków DA i AB. Odcinki CE oraz AC przecinają odcinek DF odpowiednio w punktach G i H. Oblicz pole czworokąta AHGE. Proszę o pomoc.

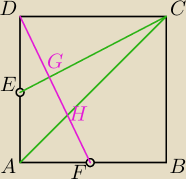
Bizon: np S_AHGE=4−S_FBCD−S_AFH−S_DEG

nokia: Bizon: Tyle to ja wiem ale nie wiem jak obliczyć pole trójkąta AHF

Bizon: a jakie kąty ma ten trójkąt Jego bok AF też znasz...

elo: Bizon: AF=1 Kąt FAH=45 Kąt AFH = 60?

Bizon: ...dokładnie −

Nokia: Bizon: Ej mam pytanie skąd wiem, że trójkąt AFD ma kąty 90, 60, 30

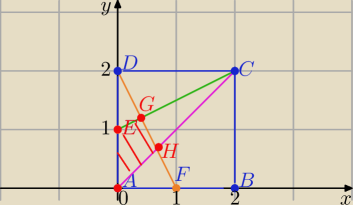Eta: Proponuję taki sposób Wykorzystując narzędzia geometrii analitycznej Umieszczam ten kwadrat w układzie współrzędnych A(0,0). B(2,0), C(2,2) , D(0,2) , E(0,1), F(1,0) Piszę równania prostych :

	1
AC: y=x . DF: y= −2x+2 , EC: y=		x+1 ( myślę ,że wiesz jak wyznaczyć te równania)
	2

rozwiązując układ równań:

	2		2
prostej DF i prostej AC otrzymasz H(		,		)
	3		3

	2		6
i prostej DF i prostej EC otrzymasz G(		,		)
	5		5

P(AHGE)= P(AHD)− P(EGD) →

	2		2		2		1
AH=[		,		] i EG=[		,		]
	3		3		5		5

AD=[0,1] ED=[0,1]

	1		2		1		2
P(AHD)=		|		| P(EGD)=		*|		|
	2		3		2		5

	1		1
P(AHD)=		P(EGD)=
	3		5

	1		1		7
tp P(AHGE)=		−		=		[j2]
	3		5		15