Tryginometria

Tryginometria Justa:

	x+π
Jak narysować funkcje f(x)=cos
	2

23 lut 19:21

Maslanek:

	x+π
to jest: f(x)=cos(		)
	2

	x
Czyli g(x)=cos		w translacji o wektor [−π,0]
	2

23 lut 19:38

ICSP:

	−π
o wektor [		, 0 ]
	2

23 lut 19:41

pigor: ...., lub

	x+π		π		x		x
cos		= cos(		+		)= −sin
	2		2		2		2

	x
i rysuj więc y= −sin		.
	2

23 lut 19:45

Maslanek: O wektor [−π,0]

	x		π
Tak miałbyś h(x)=cos(		+		)
	2		4

23 lut 19:46

ICSP: Masz racje emotka

23 lut 19:48

Justa: czy to ma być coś takiego: http://w.fotka.pl/014/053/178ccf6713.jpg

23 lut 20:33

Mila:

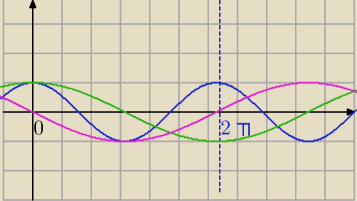y=cos(x) y=cos(x/2)

	(x+π)
y=cos
	2

23 lut 21:34

Justa:

	π
dlaczego jest ten wykres jest przesunięty o		w lewo a nie w prawo ?
	2

23 lut 21:42

Mila: f(x+2) przesunięcie o wektor [−2,0] ( 2 jednostki w lewo) f(x−2) przesunięcie o wektor [2,0] (2 jednostki w prawo) Za chwilę sprawdzę, czy dobrze wpisałam wzór, zrobię nowy rysunek z większą ilością jednostek.

23 lut 21:57

Justa: ok ok ok emotka

dziękuję

23 lut 22:04

Mila:

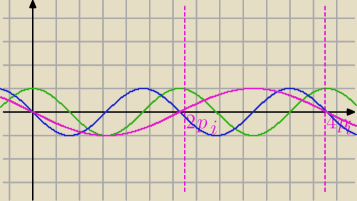
A najlepiej jak radzi Pigor y=−sin(x/2)

23 lut 22:09

Justa: wielkie dzięki emotka

23 lut 22:14

Mila:

23 lut 22:15