trygonometria
pliska: 1. Kąty ostre α i β trójkąta prostokątnego spełniają warunek sinα * tgβ = 1/2. Oblicz: a) sumę
sinusów kątów ostrych tego trójkąta b) sumę cosinusów kątów ostrych tego trójkąta
Prawidlowa odpowiedz:
a) 2√2 + 13
b) 2√2 + 13
23 lut 19:01
czarna: POPRAWKA
Kąty ostre α i β trójkąta prostokątnego spełniają
warunek sinα * tgβ = 1/3.
Oblicz: a) sumę sinusów kątów ostrych tego trójkąta b) sumę cosinusów kątów ostrych tego
trójkąta
23 lut 19:16
agulka:
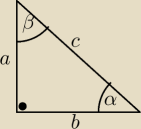
c=3b
a
2+b
2=c
2
a
2+b
2=9b
2
a
2=8b
2
a=2
√2b
| | a | | b | | 2√2b | | b | | 2√2+1 | |
sinα+sinβ= |
| + |
| = |
| + |
| = |
| |
| | c | | c | | 3b | | 3b | | 3 | |
| | b | | a | | b | | 2√2b | | 1+2√2 | |
cosα+cosβ= |
| + |
| = |
| + |
| = |
| |
| | c | | c | | 3b | | 3b | | 3 | |
23 lut 20:32
Eta:
dla kątów ostrych : sinα=cosβ , sinβ=cosα
| | sinβ | | 1 | |
sinα* tgβ= cosβ* |
| = sinβ= |
| , a=√9k2−k2=√8*k=2√2*k |
| | cosβ | | 3 | |
| | 2√2 | | 1 | | 2√2+1 | |
sinα+sinβ=cosβ+cosα= |
| + |
| = |
| |
| | 3 | | 3 | | 3 | |
23 lut 20:43