fukcje Bartek: Własności funkcji. Witam, mam problem z zadaniami z własności funkcji. Jakbyście mogli mi wytłumaczyć jak to sie robi byłbym wdzięczny. 1. Niech f:R→R będzie określona wzorem:

	2x+1
		dla x≠−2
	x+2

f(x)= 2 dla x=−2 Sprawdzić czy jest bijekcją, jeśli tak wyznaczyć f⁻¹ 2.Niech f:R→R będzie określona wzorem:

	⎧	2x+3 dla x∊R, x≠−1 x≠0
f(x)=	⎨	3 dla x=−1
	⎩	0 dla x=0

Sprawdzić czy jest bijekcją, jeśli tak wyznaczyć f⁻¹ O ile z injekcją jeszcze jako tako sobie poradzę, to dalej nie potrafie. Dodam, że chciałbym sie tego nauczyć metodą algebraiczną.

Trivial: f : X → Y iniekcja: funkcja f jest różnowartościowa suriekcja: Y = f(X) // f(X) oznacza obraz funkcji f na zbiorze X bijekcja: iniekcja + suriekcja

Bartek: to akurat wiedziałem mógłbys mi pomóc w tym, jak sie sprawdza czy dana fukncja jest surjekcją, injekcją?

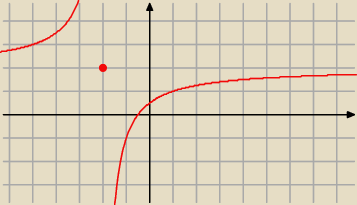
Trivial: Z iniekcją sprawa jest prosta − można robić tak jak w liceum. Jeśli chodzi o suriekcję, to trzeba wyznaczyć obraz funkcji f na zbiorze X (w tych zadaniach R).

	2x+1		3
f*(x) =		= 2 −
	x+2		x+2

	3
Funkcja f*(x) jest różnowartościowa, gdyż jest po prostu przesunięciem funkcji −		, która
	x

w oczywisty sposób jest różnowartościowa. Obrazem funkcji f* na zbiorze R\{−2} jest: f*(R\{−2}) = R\{2} Zatem jeśli dołączymy do funkcji f* przejście −2 → 2 otrzymamy funkcję różnowartościową f, taką że: f(R) = R, czyli f: R → R jest bijekcją.

Trivial: A drugie jest trywialne. Wystarczy znaleźć kontrprzykład na rzekomą iniekcję. f(0) = 0 f(−³₂) = 2*(−³₂) + 3 = 0 Wniosek: funkcja f nie jest iniekcją, a zatem nie jest też bijekcją.