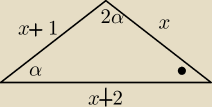
Zadanie Kostek: Jeśli mam trójkąt w którym kąt naprzeciwko najdłużego boku jest dwa razy większy od najmniejszego kąta to ile jest w miejscu kropki ? 180−3α ?

Aga1.: Tak

Kostek: Dzięki

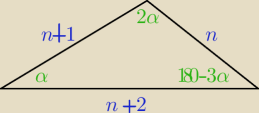
Kostek: Polecenie: Długości boków pewnego trójkąta wyrażają się kolejnymi liczbami naturalnymi. Największy kąt w tym trójkącie jest dwa razy większy od kata najmniejszego.Wyznacz długości boków tego trójkąta Z tw carnota (n+1)²=(n+2)²+n²+2(n+2)ncosα Ale co to mi da ? Proszę o tylko o naprowadzenie..... co mam robić dalej. Chcę to zrobić sam

Saizou : tw. sinusów

n		n+2
	=
sinα		sin2α

sinα(n+2)=sin2α*n sinα(n+2)=2sinαcosα*n /:sinα bo jest to kąt (0:180) n+2=2cos*n

	n+2
cosα=
	2n

wrzucając to do tw. cosinusów n²=(n+1)²+(n+2)²−2(n+1)(n+2)*cosα

	n+2
n2=n2+2n+1+n2+4n+4−2(n2+3n+2)*
	2n

	n3+5n2+8n+4
n2=2 n2+6n+5−
	n

	n3+5n2+8n+4
n2+6n+5−		=0
	n

n³+6n²+5n−n³−5n²−8n−4=0 n²−3n−4=0 (n−4)(n+1)=0 n=4 bo n>0 zatem te boki to 4,5,6 jak nie zrobiłem błędu

zawodus: kiepska wskazówka co dalej Saizou

Saizou : wiem że kiepska, dalej trzeba obliczyć całkę potrójną dziewiątego stopnia z logarytmu naturalnego granicy sinusa z pierwiastka sześciennego po obszarze omega

Kostek: A czytać potrafi napisałem wskazówkę a nie rozwiązania <facepalm>

Saizou : a co da ci wskazówka skoro źle napisałeś tw. Carnota

Kostek: To trzeba było poprawić a nie gotować pisać... Chyba napisałem naprowadzić#rozwiązać

Saizou : ale nikt nie kazał ci analizować rozwiązania

Kostek: Ja chciałem wskazówkę.. Gotowca to mogę analizować bo taki za pewne na Internecie jest...i też bym go znalazł. Ale chyba każdy chce się nauczyć.. Poradziłbym sobie jak bym dostał wskazówkę.

Saizou : zauważ że zacząłem pisać do tego czego ci brakowało, czyli to niejako wskazówka

Kostek: To można było napisać popraw twierdzenie...

zawodus: Koniec... bo ta rozmowa nie prowadzi do niczego