trygonometria Kuba:): Czzesć, może mi ktoś wytłumaczyć jak zrobić to zadanie? Oblicz pozostałe wartości funkcji trygonometycznych kata alfa, wiedząc, że : ctgα=3

	45 28
ctgα=

Umiem zrobić, gdy wiadomo, sinus lub cosinus, ale z tym mam problem To pilne, więc jeśli można prosić to proszę o pomoc

Aga1.:

	cosα		3
ctgα=		=
	sinα		1

cosα=3sinα podstaw do 1 trygonometrycznej i sin²α+9sin²α=1 dokończ b)

45 28		45!
	=		=
		28!*(45−28)!

PW: To są dwa zadania. Z którym masz problem?

Kuba:): No własnie z tymi dwoma. I własnie dotarłem do tego co Pani napisała: sin2α+9sin2α=1, a dalej nie wiem co mam robić

PW: Masz problem typu "ile to jest krowa dodać 9 krów"?

Kuba:): no, po prostu wyjdzie 10 sinα²=1,no i co dalej?

Aga1.: 10sin²α=1

	1
sin2α=
	10

licz dalej.

Kuba:): sinα²=10−1 sinα²=9 sinα=3 v −3 Tak dobrze?

PW: Aga, on ma kłopoty ze wszystkim.

Kuba:): dobra, jak nie chce pomóc to nie musisz tu nic pisać, dzięki!

Antek: Co Ty wypisujesz . Przeciez jestes w 2 lub 3 klasie techniku czy liceum Zalamac sie idzie . Przeciez nie masz 10+sin²x=1 tylko masz mnozenie to 10sin²x=1 to sin²x= ile

Kuba:):

	1 10
jeśli sin2α=

	3 √10
cosα=

Eta: Dobre Aga1 z tymi silniami

Antek: Ulamki zapisuj za pomoca duzej litery U bo to co piszesz w tych nawiasach to jesy symbol newtona (a to sie inaczej liczy ) cos x dobrze jednak wrocmy do sinusa

	1
sin2x=		to sinx=√1/10 lub −√1/10 ktora wartosc przyjmujemy
	10

Mila: Kuba, ułamki piszemy za pomocą dużej litery Upotem piszemy {1}{10} i mamy:

	1
sin2α=
	10

	9
cos2α=
	10

	1
cosα=		dla kąta ostrego
	√10

Antek: No to napisz jeszcze ile wynosi tg x

Kuba:):

	1
tgx to przeciwieństwo ctg, więc jeśli ctg=3, to tng=
	3

Antek: Dobrze .

Kuba:):

	1
no dobrze, ale nadal średnio wiem skąd wyszło, że sin2α=
	10

Antek: Chociaz tego teraz nie ucza bo uczniom jest ciezko to moze sobie to gdzies zapisz (moze sie przyda ) Jesli masz dany ctgx to

	1
sinx=
	√1+ctg2x

	ctgx
cosx=
	√1+ctg2x

Jeszeli masz dany tgx to wtedy

	tgx
sinx=
	√1+tg2x

	1
cosx=
	√1+tg2x

Kuba:): Dobrze, dzięki. Zapisane

Antek:

	cosx		3
ctgx=		=		bo masz podane ze ctgx=3
	sinx		1

	cosx		3
to z rownosci		=		cosx=3sinx
	sinx		1

Jedynka trygonometryczna sin²x+cos²x=1 ale nasze cosx=3sinx i teraz sin²x+(3sinx)²=1 to sinx+3²*sinx²=1 to sin²x+9*sin²x =1 dalej powinno byc juz wiadomo

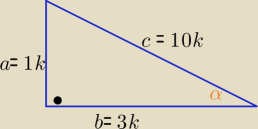
Eta: α −− kąt ostry

	b		3k
ctgα=		=3=		, b=3k , a=1k , c2=k2+9k2 ⇒ c=√10
	a		1k

	1		1		3
tgα=		, sinα=		, cosα=
	3		√10		√10

Antek: Przypatrz sie dobrze na ten rysunek i go przeanalizuj bo nie wiem czy tak pokazuja uczniom w szkole , a powinni wtedy by nie bylo problemow z takimi zadaniami

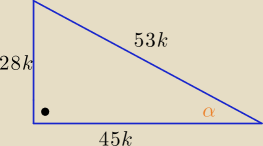
Eta: α −−− kąt ostry

	45
ctgα=		c=.....
	28

	28		28		45
tgα=		, sinα=		, cosα=
	45		53		53

Kuba:): Dobra załapałem, dzięki