trygonometria tyu: jakaś podpowiedź do tego zadania IsinxI=IcosxI ?

Ajtek: Najprościej graficznie .

tyu: graficznie to wiem, że się da, ale czy algebraicznie nie da rady?

Ajtek: Da radę, myśl .

tyu: to trzeba rozwiązać równanie cosx=sinx, ale rozwiązania są tylko w I i II ćwiartce ?

ICSP: Dwa przypadki : 1^o cosx = 0 2^o cosx ≠ 0

tyu: może chociaż wzory jak te 2 przypadki mają wyglądać (rozwiązać spróbuję sam), bo nie wymyślę tego

ICSP: a jakie wartości może przyjąć sinx gdy cosx = 0 ?

tyu:

	π
gdy cosx=0, to sinx =		= 1
	2

Ajtek: lub −1 .

tyu: no tak, nie spojrzałem dalej na wykres czyli te wzory to sinx= 1 lub sinx = −1, chyba nie ?

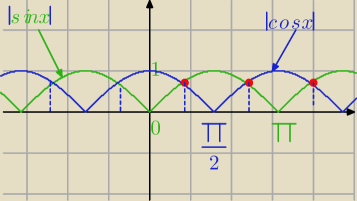
Mila: Rozwiąż równanie: IsinxI=IcosxI Z wykresu:

	π
sinx=cosx dla x∊(0,		)
	2

	π
x=
	4

odp.

	π		kπ
x=		+
	4		2

tyu: dziękuję za wyjaśnienie

PW: Ale myśli ICSP nie podjąłeś. Trzeba było zwyczajnie podzielić obie strony przez cosx i rozwiązać równanie |tgx| = 1.

tyu: czyli w ten sposób IsinxI=IcosxI / cosx ItgxI = 1 => tgx = 1 lub tgx = − 1

	π		−π
x =		lub x =
	4		4

PW: No pewnie, o wiele łatwiej zauważyć rozwiązanie. Pamiętaj o okresowości i spróbuj zobaczyć możliwość zapisania obu serii rozwiązań za pomocą jednego wzoru, żeby porównać z wynikiem Mili.

ZKS: Można też podnieść obustronnie do kwadratu przenieść wszystko na jedną stronę i skorzystać ze wzoru na cos(2x).

tyu: podnoszenie do kwadratu obu stron, to będzie w ten sposób ? IsinxI=IcosxI /² sin²x=cos²x sin²x−cos²x=0

	1
sin2x−1+sin2x=0 2sin2x=1 sin2x=
	2

	√2		−√2
sinx=		lub sinx =		czyli
	2		2

	π		−π
x =		lub x =
	4		4

ICSP: https://matematykaszkolna.pl/strona/1602.html