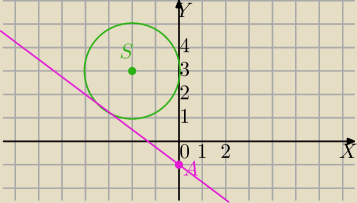
styczna do okręgu ;;;: W układzie współrzędnych narysuj okrąg o równaniu (x+2)²+(y−3)²=4 oraz zaznacz punkt A=(0,−1). Prosta o równaniu x=0 jest jedną ze stycznych do tego okręgu przechodzącą przez punkt A. Wyznacz równanie drugiej stycznej do tego okręgu, przechodzącej przez punkt A. Umiem to narysować, ale nie wiem jak wyznaczyć. Jedyne co mam to: y=ax+b, więc −1=b.

Mila: s: y=ax−1 Podstawiamy do równania okręgu (x+2)²+(ax−1−3)²=4 x²+4x+4+a²x²−8ax+16=4 x²(1+a²)+x*(4−8a)+16=0 Aby prosta była styczna to musi mieć jeden punkt wspólny z okregiem ⇔ Δ=0⇔Δ=(4−8a)²−4*16*(1+a²)=0 16−64a+64a²−64−64a²=0 16−64a−64=0⇔64a=−48

	−3
a=
	4

	−3
s: y=		x−1
	4

Posprawdzaj rachunki. II sposób z odległości stycznej od S

;;;: dziękuję : )

Mila: