plani
bezendu:
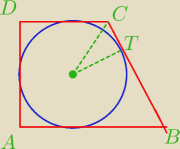
W trapez prostokątny ABCD wpisano okrąg, przy czym punkt S jest środkiem tego okręgu, a punkt
T jest punktem styczności okręgu wpisanego z dłuższym ramieniem BC . Oblicz pole tego
trapezu, jeśli |SC | = 10 i |BT | = 8
√5
?
22 lut 20:18
zawodus: kąt BSC jest prosty

22 lut 20:43
bezendu:
Dzięki zobaczymy czy ta podpowiedź coś da

22 lut 20:46
Mila:
Przypomnij sobie wzór o wysokości poprowadzonej z wierzchołka kata prostego w Δprostokatnym.
22 lut 21:29
bezendu: Dziękuję już się uporałem z tym zadaniem..
22 lut 21:32
Mila:
Coś słabo dzisaj działasz, spadek motywacji, czy formy?
22 lut 23:53
bezendu: jestem na forum, ale chyba pierwsza opcja, już coraz trudniejsze robią się te zadania.
22 lut 23:54
Mila:
Rozwiązuj ze stopniowaniem trudności.
Wpisz jutro te z problemami. Nie wiem jak to zadanko rozwiązałeś?
22 lut 23:57
bezendu:
Z podobieństwa i pitagorasa według wskazówki zawodusa.
22 lut 23:59
Eta:

23 lut 00:04
bezendu:
Rozwiązuję ze stopniowaniem ale już przy tych z 3 gwiazdkami mam problemy
23 lut 00:04
Mila:
Do jutra.
Dobranoc. Widzę, że Eta zawitała do Ciebie. Zróbcie cos z trapezikiem, bo to zadanko z
równymi polami to Ci jeszcze nie wyszło a tam jest średnia ...
23 lut 00:14
bezendu:
Mila Dobranoc. Z tym trapezem to już 3 razy robię i nie wychodzi
23 lut 00:17
Mila:
Jutro zrobisz na pewno.
23 lut 00:18
Eta:
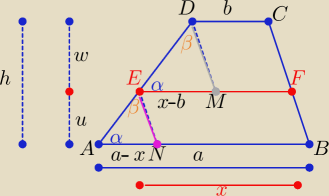
Dorysowałam odcinki : DM ∥ CF i EN ∥ FB
|AN|=a−x , |EM|=x−b
P(ABEF)=P(EFCD)
| | a+x | | x+b | | a+x | | w | |
|
| *u= |
| *w ⇒ |
| = |
| |
| | 2 | | 2 | | x+b | | u | |
z podobieństwa trójkątów ANE i EMD z cechy (kkk)
| | a+x | | x−b | |
to: |
| = |
| ⇒ a2−x2=x2 −b2 ⇒ 2x2=a2+b2 |
| | b+x | | a−x | |
| | a2+b2 | |
|EF|=x=√ |
| −−−− średnia kwadratowa długości podstaw trapezu |
| | 2 | |

dla
bezendu
23 lut 01:11
zawodus: Świetne rozwiązanie muszę przyznać, że lepsze od mojego

 Eta
Eta
23 lut 09:41
Saizou :
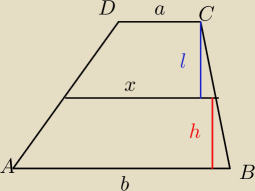
| 1 | | (b+x) | | P | |
| P= |
| h →h= |
| |
| 2 | | 2 | | b+x | |
| | (a+b) | | P | | P | |
P= |
| ( |
| + |
| )=....= |
| | 2 | | b+x | | a+x | |
| | (a+b)2+2x(a+b) | | a2+b2 | |
P* |
| ⇒2a+2x2=(a+b)2⇒x=√ |
| |
| | 2ab+2x2+2x(a+b) | | 2 | |
23 lut 10:01
Saizou : tam miało być
2ab+2x2=(a+b)2
23 lut 10:02
zawodus: Ściągałeś

23 lut 10:05
Saizou : nie, znałem tę metodę, mieliśmy ją kiedyś na lekcji xd
23 lut 10:07
bezendu:
Dzięki ale sam chciałem dziś to zrobić jeszcze raz..

23 lut 16:06
Eta:
Napisałeś,że "rozwiązywałem trzy razy i....... nic"

23 lut 16:08
bezendu: Ale nie napisałem, że chcę rozwiązanie na tacy ?
23 lut 16:09
Mila:
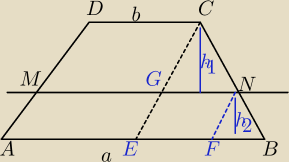
Podpowiedź.
|MN|=e
GN=e−b
FB=a−e
ΔGNC∼ΔFBN
23 lut 16:22
Eta:
Witaj
Mila 
Patrzyłaś na moje rozwiązanie? ..... przecież to, to samo co podałam, tylko inne oznaczenia

23 lut 16:27
Mila:
Witam, właśnie nie spojrzałam. Pozdrawiam.

23 lut 16:30
bezendu:
I ja skorzystam z podpowiedzi a nie gotowca.
23 lut 16:32
bezendu: Dziękuję ten dowód już zrobiony

23 lut 16:49
Eta:
@
bezendu 

23 lut 16:50
bezendu: Eta zobacz do mojego innego tematu.
23 lut 16:53
 W trapez prostokątny ABCD wpisano okrąg, przy czym punkt S jest środkiem tego okręgu, a punkt
T jest punktem styczności okręgu wpisanego z dłuższym ramieniem BC . Oblicz pole tego
trapezu, jeśli |SC | = 10 i |BT | = 8√5
?
W trapez prostokątny ABCD wpisano okrąg, przy czym punkt S jest środkiem tego okręgu, a punkt
T jest punktem styczności okręgu wpisanego z dłuższym ramieniem BC . Oblicz pole tego
trapezu, jeśli |SC | = 10 i |BT | = 8√5
?



 Dorysowałam odcinki : DM ∥ CF i EN ∥ FB
|AN|=a−x , |EM|=x−b
P(ABEF)=P(EFCD)
Dorysowałam odcinki : DM ∥ CF i EN ∥ FB
|AN|=a−x , |EM|=x−b
P(ABEF)=P(EFCD)
 dla bezendu
dla bezendu

 Eta
Eta




 Podpowiedź.
|MN|=e
GN=e−b
FB=a−e
ΔGNC∼ΔFBN
Podpowiedź.
|MN|=e
GN=e−b
FB=a−e
ΔGNC∼ΔFBN
 Patrzyłaś na moje rozwiązanie? ..... przecież to, to samo co podałam, tylko inne oznaczenia
Patrzyłaś na moje rozwiązanie? ..... przecież to, to samo co podałam, tylko inne oznaczenia




