logarytmy
Radek:
Zaznacz w układzie współrzędnych zbiór punktów (x,y) , dla których współrzędne spełniają
nierówność logx y < logy x
?
22 lut 20:14
Hajtowy:
Nie wiem czy dobrze myślę...
Założenia:
x,y > 0
x ≠ 1
y ≠ 1
| | logxx | | 1 | |
logxy < |
| = |
| |
| | logxy | | logxy | |
Podstawić warto, że t=log
xy i dokończyć
22 lut 20:18
bezendu: Przepisałeś z zadania info
22 lut 20:19
Radek:
No właśnie Hajtowy...
22 lut 20:22
Hajtowy:
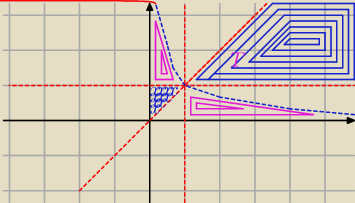
To co na różowo i niebiesko ma być zamalowane − jest to ten obszar.
Ta niebiesko−czerwona linia − ma być przerywana
22 lut 20:25
Radek: Fajnie, że nic nie wytłumaczyłeś.....
22 lut 20:27
Mila:
Radek, zostaw to zadanie. To podwyższony poziom trudności.
22 lut 20:39
Radek: A jak będzie na maturze to co ?
22 lut 20:39
Mila:
Nie będzie, możemy wrócić pod koniec kwietnia do tego.
Mogę ci podać prawdopodobne zadania tego typu ( nieco łatwiejsze).
1) Zaznacz w układzie współrzędnych zbiór punktów (x,y) , dla których współrzędne spełniają
warunki:
b) log
2(x
2+y)≤1
c)log
1/4(x
2+y
2)≥−1
22 lut 20:48
Radek:
To zadania mam ze zbioru Pazdro, a robię jak najwięcej arkuszy.
To może Pani mi pomóc w tych 3 ?
22 lut 20:52
Mila:
Jakie masz swoje propozycje, co najpierw trzeba zrobić?
22 lut 20:54
Radek:
Najpierw trzeba ustalić dziedzinę
?
22 lut 20:55
zawodus: skoro to funkcja to tak
22 lut 21:04
Mila:
Nie ma w mianowniku x−sa. Dobrze zacząłeś.
Popraw i wyznacz dziedzinę.
22 lut 21:04
Radek:
x>1 i y>0
22 lut 21:07
Mila: Dobrze, czyli:
D: x>1 i y>0
Teraz drugi warunek, rozwiązuj rownanie.
22 lut 21:11
22 lut 21:13
Mila:
Druga linijka źle. Najpierw zwijasz logarytmy, potem porównujesz liczby logarytmowane.
22 lut 21:14
22 lut 21:18
22 lut 21:30
Radek:
| | x−1 | |
No tak to samo wyszło co Pani |
| =1 |
| | 2y | |
x−1=2y
22 lut 21:34
Mila:
Teraz narysuj w układzie wsp. uwzględniając dziedzine.
22 lut 21:38
Radek:
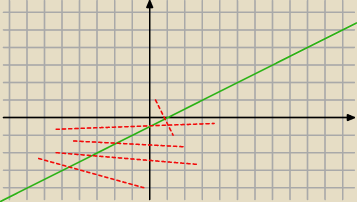
Ten obszar nie zakreskowany
22 lut 21:41
Mila:
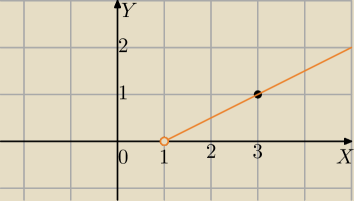
22 lut 21:45
Radek: Czemu Pani zaznaczyła ten czarny punkt ?
22 lut 21:46
Mila:
Jako punkt wykresu , rysowałam ręcznie, potrzebne dwa punkty półprostej.
22 lut 21:47
Radek:
log2(x2+y)≤1
x2+y>0
?
22 lut 21:50
Mila:
Czyli jak jest dzziedzina ?
22 lut 21:53
Radek: x2>y ? D=R ?
22 lut 21:55
Mila:
Nie,
D: y>−x2
Rozwiązuj dalej , porównanie liczb logarytmowanych.
22 lut 22:08
Radek:
log2(x2+y)≤log22
x2+y≤2
y<−x2+2?
22 lut 22:11
Mila:
y≤−x2+2 i y>−x2
Mam narysować?
22 lut 22:13
Radek: Czemu Pani dzieli na dwa przypadki ?
22 lut 22:15
Mila:
Jak dzielę,(?) uwzględniam dziedzinę.
22 lut 22:17
Radek:
czemy dziedzina to
y>−x2 a nie x2>y ?
22 lut 22:18
Mila:
g(x)=log2(x2+y)
x2+y>0⇔y>−x2
22 lut 22:23
Radek: zawsze po lewej musi być y ?
22 lut 22:28
Mila:
Tutaj tak, bo chcemy narysować wykres tej krzywej.
22 lut 22:30
Radek:
Narysować potrafię ale potem jak wybrać ten prawidłowy obszar ?
22 lut 22:31
Radek:
?
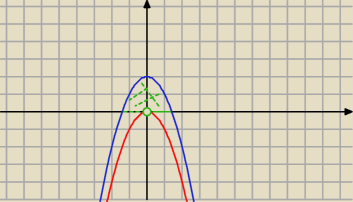
22 lut 22:37
Mila:
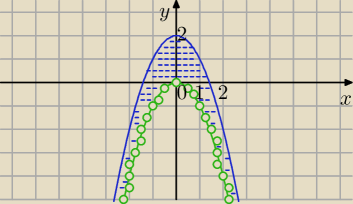
y≤−x
2+2 i y>−x
2
y>−x2 punkty powyżej paraboli , bez punktów leżących na tej paraboli
i
y≤−x2+2 punkty poniżej paraboli
22 lut 22:53
Radek:
log1/4(x
2+y
2)≥−1
x
2+y
2≥0
to wywalam punkt (0,0) ?
log
1/4(x
2+y
2)≥log
1/44
x
2+y
2≥4
22 lut 22:58
Mila:
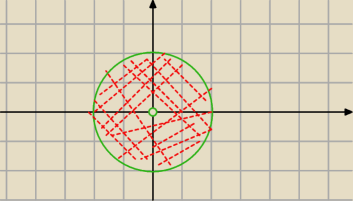
D: x2+y2>0 cała płaszczyzna bez punktu (0,0)
log1/4(x2+y2)≥log1/4(4) funkcja malejąca ⇔
x2+y2≤4 wnętrze koła x2+y2=22 bez punktu(0,0)
Przeczytaj dokładnie, bo popełniłeś błędy.
Obszar zaznaczony dobrze.
22 lut 23:12
Radek:
To jeśli funkcja jest malejąca to zmieniam znak nierówności ?
22 lut 23:14
Mila:
Tak.
22 lut 23:21
Radek:
A mogę jeszcze jedno zadanie tego typu wstawić jeśli Pani jeszcze jest ?
22 lut 23:22
Mila:
Tak.
22 lut 23:22
Radek:
W prostokątnym układzie wsp przedstaw zbiór wszystkich punktów płaszczyzny spełaniających
warunki
| x+3 | |
| =logx+2(y+2) i y2≤36 |
| log2(x+2) | |
najpierw log
2(x+2)>0
x+2>0
x+2≠1
y+2>0 ?
22 lut 23:26
Mila:
log2(x+2)≠0⇔x+2≠1⇔x≠−1
x+2>0⇔x>−2
y+2>0⇔y>−2 i y2≤36
Teraz wyznacz y ;
22 lut 23:38
Radek: Nie rozumiem pierwszej linijki ?
log2(x+2)≠0 bo mianownik
x+2>0 dziedzina logarytmu ?
22 lut 23:41
Mila:
Tak.
22 lut 23:50
Radek:
A to nie powinno być
| x+3 | | log2(y+2) | |
| = |
| |
| log2(x+2) | | log2(x+2) | |
x+3=log
2(y+2) ?
22 lut 23:53
Mila:
Dobrze, dalej.
22 lut 23:55
Radek:
Ale jak dalej to rozpisać
log2 żeby było x+3 ?
22 lut 23:56
Mila:
Z definicji logarytmu.
2x+2=y+2
22 lut 23:57
Radek:
Jak z definicji ? i ja mam x+3
23 lut 00:01
Radek: ?
23 lut 00:10
Mila:
Tak, zrobiłam literówkę.
2x+3=y+2
23 lut 00:12
Radek:
Ale nadal niestety nie wiem co i jak ?
23 lut 00:12
Mila:
log2(8)=3 bo 23=8
y=2x+3−2
To trzeba narysować uwzględniając dziedzinę.
Narysuj, jutro sprawdzę.
DOBRanoc.
23 lut 00:18
Radek:
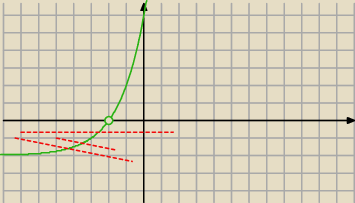
23 lut 00:27
zawodus: A co z warunkiem y2<=36?
23 lut 09:47
Radek:
Czyli wracając do dziedziny x∊(−2,∞)/{−1} ?
23 lut 14:40
Mila:
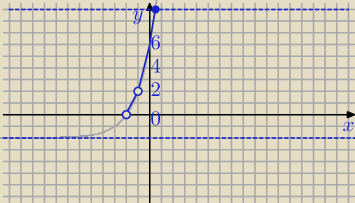
D:
X>−2 i x≠−1 i −2<y≤6
23 lut 16:05
Radek:
−2<y≤6 ?
23 lut 16:08
Mila:
tak.
23 lut 16:23
Radek:
Ale dziedzina y>−2 ?
23 lut 16:24
Mila:
Przecież miałeś warunek y+2>0⇔y>−2
23 lut 16:31
Radek:
Tak.
23 lut 16:31
Radek:
To skąd w dziedzinie y≤6 ?
23 lut 16:54
Mila:
Bo był warunek y2≤36⇔y∊<−6,6>
23 lut 16:59
Radek:
A ja go wgl nie brałem do dziedziny.
23 lut 17:01
Mila:
Czytaj uważnie treść zadania.
23 lut 17:06
Radek:
Dobrze dziękuję
23 lut 17:08