dwusieczna w trojkacie wera: jak znalezc wspolrzedne punktu przeciecia dwusiecznej kata A z przeciwleglym bokiem BC trojkata ABC (A=4,1, B=7,5, C=−4,7)?

Cash18: Wylicz równania AC i AB i zauważ że są one oddalone od dwusiecznej w takiej samej odległości. Myślę że sobie poradzisz. Pozdrawiam

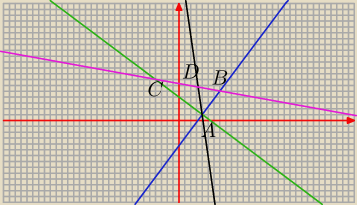
Janek191: A = ( 4; 1) B = ( 7; 5) C = ( − 4; 7 ) Prosta AB

	5 −1		4
a =		=
	7 − 4		3

y = a x + b

	4		3		16		13
1 =		*4 + b ⇒ b =		−		= −
	3		3		3		3

	4		13
y =		x −
	3		3

=================== Prosta AC

	7 −1		3
a1 =		= −
	− 4 − 4		4

	3
y = −		x + b1
	4

	3
7 = −		*(−4) + b1
	4

b₁ = 7 − 3 = 4

	3
y = −		x + 4
	4

==============] Te proste są prostopadłe Prosta AD, gdzie D punkt przecięcia się dwusiecznej kąta ∡ A z bokiem BC y = a₂ x + b₂ Kąt między prostą AB i prostą AD ma 45 ^o oraz

	a2 − 43
tg φ = I		I = tg 45o = 1
	1 + 43*a2

	4
a2 − 43 = 1 +		*a2
	3

a₂ = − 7 −−−−−−−−−−−−−− y = − 7 x + b₂ 1 = −7*4 + b₂ b₂ = 29 y = − 7 x + 29 =========== Prosta BC ma równanie

	2		69
y = −		x +
	11		11

===================== D − punkt wspólny pr BC i pr AD y = − 7 x + 29

	2		69
y = −		x +
	11		11

−−−−−−−−−−

	2		69
− 7 x + 29 = −		x +		/ * 11
	11		11

− 77 x + 319 = − 2 x + 69 − 75 x = − 250 / ( − 25) 3 x = 10

	10		1
x =		= 3
	3		3

	10		70		87		17		2
y = − 7*		+ 29 = −		+		=		= 5
	3		3		3		3		3

	1		2
D = ( U{ 3		; 5		)
	3		3

========================

wera: dziękuję, obliczylam równania AC= − 13/4 x +11 AB= 1/3 x +8/3 nie rozumiem wyliczania rownan co dalej?

wera: juz patrze, dzieki

Janek191: Kliknij po lewej stronie na: geometria analityczna kąt między prostymi

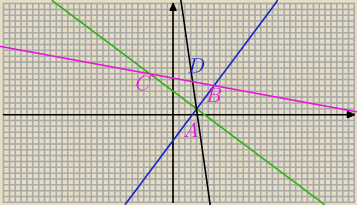
Janek191: II sposób: A = ( 4; 1) B = ( 7; 5) C = ( − 4; 7 ) Wyznaczamy prostą AB : y = a x + b 1 = 4a + b 5 = 7a + b −−−−−−−−− odejmujemy stronami 5 − 1 = 7a + b − 4a − b 4 = 3a

	4
a =
	3

	4		3		16		13
b = 1 − 4 a = 1 − 4*		=		−		= −
	3		3		3		3

	4		13
y =		x −
	3		3

−−−−−−−−−−−−−−−−−−−−

	y2 − y1
Wyznaczamy prostą AC ( innym sposobem ) : y − y1 =		*( x − x1)
	x2 − x1

	7 − 1
y − 1 =		*(x − 4)
	− 4 − 4

	6
y = −		*( x − 4) + 1
	8

	3
y = −		x + 3 + 1
	4

	3
y = −		x + 4
	4

−−−−−−−−−−−−−−−−−−− Prosta AB w postaci ogólnej :

	4		13
y =		x −		/ * 3
	3		3

3 y = 4 x − 13 4x − 3y − 13 = 0 ============ Prosta AC w postaci ogólnej :

	3
y = −		x + 4 / * 4
	4

4 y = − 3 x + 16 3 x + 4 y − 16 = 0 ============== Korzystamy z wzoru na dwusieczne : Mamy

I 4x − 3y − 13 I		I 3 x + 4 y − 16 I
	=		/ * 5
√42 + (−3)2		√32 + 42

I 4 x − 3y − 13 I = I 3 x + 4 y − 16 I Wyznaczamy dwusieczną I 4 x − 3 y − 13 I = 3 x + 4 y − 16 4 x − 3 y − 13 = − ( 3 x + 4 y − 16) 4 x − 3 y − 13 = − 3 x − 4 y + 16 lub 4 x − 3 y − 13 = 3 x + 4 y − 16 7 x + y − 29 = 0 lub x − 7 y + 3 = 0

	1		3
y = − 7 x + 29 lub y =		x +		− równanie II dw.
	7		7

=========== więc prosta AD ma równanie: y = − 7 x + 29 ============== Wyznaczam jeszcze równanie prostej BC

	7 − 5
y − 5 =		*( x − 7)
	− 4 − 7

	2
y = −		( x − 7) + 5
	11

	2		14		55
y = −		x +		+
	11		11		11

	2		69
y = −		x +
	11		11

===================== Znajduję punkt wspólny prostych : AD i BC : y = − 7 x + 29

	2		69
y = −		x +		/ * 11
	11		11

−−−−−−−−−−−−−−−− y = − 7 x + 29 11 y = − 2 x + 69 −−−−−−−−−−−− 11*( − 7 x + 29) = 2 x + 69 − 77 x + 319 − 2x = 69 − 75 x = 69 − 319 = − 250 / : ( − 25) 3 x = 10

	10		1
x =		= 3
	3		3

==========

	10		70		87		17		2
y = − 7*		+ 29 = −		+		=		= 5
	3		3		3		3		3

================================== Odp.

	1		2
D = ( 3		; 5		)
	3		3

========================