nierówność z modułem...
moduły, potęgi nierównośći: Podaj zbiór rozwiązań podanej nierówności
JAK SIĘ ZA TO ZABRAĆ
(|x|−1)
2014*(|x|−2)
2014>0
22 lut 17:18
PW: Podpucha. Gdyby było (u−1)2(u−2)2 > 0, to wiedzielibyśmy?
22 lut 17:22
moduły, potęgi nierównośći:
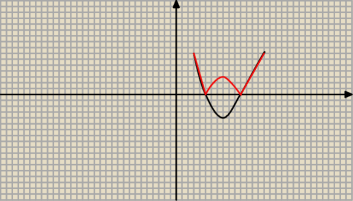
taki przykład tez jest.. wtedy ((u−1)(u−2))
2 mamy funkcję kwadratową która część ujemną odbija
od osi ?
22 lut 17:25
PW: Jak widzę to "odbijanie", to mam uczucia mieszane. I z powodu słownictwa, i z powodu metody. Po
co zaraz wykresy i armaty?
Iloczyn dwóch wyrażeń ma być dodatni (mówię o przykładzie z 17:22). I jest, bo te wyrażenia są
kwadratami. Jedyny wyjątek kiedy otrzymamy zdanie fałszywe będzie wtedy, gdy jedno z tych
wyrażeń będzie zerem:
u = 1 lub u = −2.
22 lut 17:29
PW: Tfu, ze złości pomyliłem się:
u=1 lub u = 2.
Złoszczę się na to "odbijanie" − kto to wymyślił? Potem pytają kandydata o symetrię osiową, a
ten robi baranie oczy.
22 lut 17:31
moduły, potęgi nierównośći: chyba rozumiem dzięki, wystraszyło mnie to trochę i myślałem że inaczej trzeba się za to
zabierać a tu tylko tyle wystarczy. Dzięki
22 lut 17:33
moduły, potęgi nierównośći:
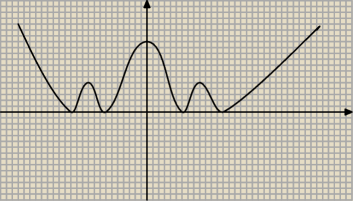
dla (|x|−1)
2014(|x|−2)
2014>0
22 lut 18:06
moduły, potęgi nierównośći:
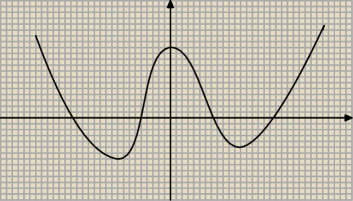
dla (|x|−1)
2013(|x|−2)
2013>0
22 lut 18:08
PW: Ale po co Ty to rysujesz? Miałeś podać zbiór rozwiązań nierówności ==== dla jakich x nierówność
jest prawdziwa. Ano dla wszystkich oprócz tych, dla których
|x| = 1 ⋁ |x| = 2
Rozwiąż to i udziel odpowiedzi.
22 lut 18:12
moduły, potęgi nierównośći:
dla (|x|−1)
2014(|x|−2)
2013>0
22 lut 18:13
moduły, potęgi nierównośći:
oraz
dla (|x|−1)
2013(|x|−2)
2014>0
gdzie w każdym przykładzie punkty przecięcia z osią ox są to odpowiednio −2;−1;1;2 . jak widać
są symetryczne względem osi oy, więc najpierw wystarczy sprawdzić co się dzieje dla |x| >0 na
prawo od osi oy, i analogicznie w lewo gzie x są ujemne. pamiętając jak zachowuje się funkcja
o wykładniku parzystym i odpowiednio nieparzystym .
Prawda ?
22 lut 18:18