Maturalne do sprawdzianu K. PAZDRO [pozdro xd] Hajtowy: Mam kilka zadań z arkusza maturalnego K. PAZDRO − których nie umiem zrobić... Zadanie 1

	1
Liczba 4		* 3√4 = 6√4 * 3√4 = ...
	6

Może i mam braki w potęgach, ale nwm czemu tu ma wyjść 2. Zadanie 2 http://www.ufast.eu/pics/339170Zadanie_2.jpg Zadanie 3

	2
Odwrotnością liczby		jest liczba:
	√3−1

Tego to już kompletnie nie wiem ... Zadanie 4 http://www.ufast.eu/pics/820367Zadanie_4.jpg Zadanie 5 Wykres funkcji liniowej f(x) = (1−m)x + m przechodzi przez I, II i III ćwiartkę układu współrzędnych, wtedy i tylko wtedy, gdy: A) m ∊ (−oo ; 1) B) m ∊ (−1;0) C) m ∊ (0;+oo) D) m ∊ (0;1) Tego też nie wiem, strzelałem... Zadanie 6 Dany jest ciąg (a_n), w którym a_n=(−1)ⁿ * (n−1), n ∊ N₊ . Jeśli k jest liczbą naturalną nieparzystą, to: A) a_k+1=−k B) a_k+1=k C) a_k+1=k−2 D) a_k+1=−k+2 Zadanie 7 Trzeci wyraz pewnego ciągu geo jest równy 6, a szósty wyraz ma wartość (−0,75). Iloraz tego ciąu jest równy ... ? Zadanie 8 http://www.ufast.eu/pics/454060Zadanie_8.jpg Zadanie 9 Figura płaska F₁ jest podobna do figur F₂. Obwód figury F₁ stanowi 40% obwodu F₂ , zaś pole figury F₁ wynosi 8. Pole figury F₂ jest równe.... ? Zadanie 10 Pole powierzchni bocznej stożka wynosi 18π. Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole przekroju jest równe...? Na razie tyle Proszę o pomoc − rozpisanie mi tych zadań. Jako maturzysta powinienem umieć to zrobić a jednak nie potrafię ...

asdf: 4^1/6 * 4^1/3 = 4^{1/6 + 1/3} = 4^1/2 = 2 ...

Aga1.: 3)

	a		b
Odwrotnością liczby		jest		, gdy ai b≠0
	b		a

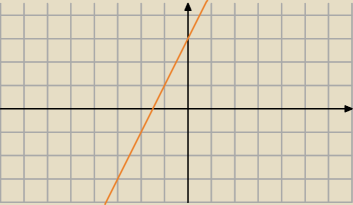
Lorak: 5. Musi być rosnąca i f(0)>0, więc pasuje tylko odpowiedź D

Trivial: 6) a_2k+1 = ?

	a6		a0q6		−0.75
7)		=		= q3 =		→ q = ?
	a3		a0q3		6

Trivial: Jednak w szóstym nie doczytałem. a_k+1 = a_(2m−1)+1 = a_2m = .. Potem podstawić z powrotem 2m−1 = k

Hajtowy: Jeszcze tam kilka jest, ale dziękuje za pomoc w tych

asdf: Jak będę mieć chwilę to zainteresuje się resztą

Trivial: 4) Widać, że funkcje są przesunięte, pozostaje ustalenie wzoru. Można wybrać jeden punkt i zobaczyć co trzeba zrobić żeby uzyskać taką wartość na drugim wykresie. Weźmy g(1). Punkt ten odpowiada f(3), zatem g(x) = f(x+2).

PW: Zadanie 9. Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa. Stosunek obwodów jest równy skali podobieństwa. Obwód F₁ = 0,4 obwodu F₂. Skala k podobieństwa przekształcającego F₁ na F₂ jest równa k = 0,4

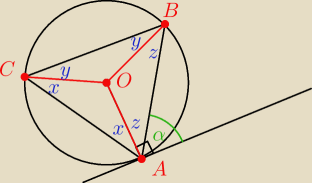
Trivial: Naszą niewiadomą jest kąt x+z = ?. Dane: α = 50^o, z+y = 75^o. Sumując wszystkie kąty w trójkącie: 2x + 2y + 2z = 180^o x = 90^o − (y+z) = 15^o z = 90^o − 50^o = 40^o x+z = 55^o.

Trivial: Zapomniałem napisać, że to zadanie 8.

Hajtowy: No pięknie Dziękuję wszystkim za zaangażowanie i pomoc

asdf: 6 b?

Hajtowy: asdf tak − chcesz rozpisać?

zawodus: A jest problem?

Hajtowy: Jest

zawodus: a_n=(−1)ⁿ * (n−1), n ∊ N₊ liczymy a_k+1 a_k+1=(−1)^k+1*(k+1−1) = (−1)^k+1*k Teraz patrzymy jakie było k (liczba nieparzysta) − zatem k+1 jest parzyste a_k+1=k, ((−1) podniesione do parzystej potęgi daje 1)

Hajtowy: Dziękuję

Hajtowy: Zadanie 9 Figura płaska F₁ jest podobna do figur F₂. Obwód figury F₁ stanowi 40% obwodu F₂ , zaś pole figury F1 wynosi 8. Pole figury F₂ jest równe.... ? Niestety PW nie ma takiej odpowiedzi. 50,40,25,20 − tylko takie ABCD jest

Piotr 10:

0,4F2
	=k
F2

	2
k=
	5

Pf1
	=k2
Pf2

P_f2=8*25/4=50

Hajtowy:

	Pf1
Skąd wiadomo, że		= k2?
	Pf2

Piotr 10: Stosunek pół figur podnych jest zawsze równy kwadratowi skali podobieństwa

Hajtowy: A to dla mnie nowość xd

Piotr 10: Serio ? wyprowadz sobie to zaleznosc najlepiej,