Analityczna czopo: Wyznacz równanie prostej przechodzącej przez punkt (2,−⁵₂), której odległość od punktu (2,4) jest równa √13

J: Ax + By + C = 0 , musisz wyznaczyć A i B wykorzystując podane dane w treści zadania.Wzory masz w innym poście

czopo: Dzięki za oba posty, spróbuję sie z oboma problemami zmierzyć

czopo: Nie zrobie tego niestety, prosiłbym jednak o pomoc z jakims objasnieniem

Mila:

	−5
A(2,		), B(2,4)
	2

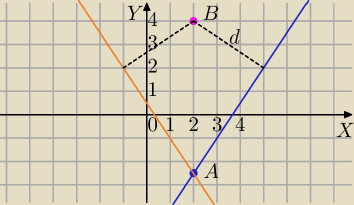
y=ax+b −postać kierunkowa

−5
	=2a+b
2

	−5
b=		−2a
	2

	−5
y=ax+		−2a /*2
	2

2y=2ax−5−4a 2ax−2y−5−4a=0 równanie prostej − postać ogólna

	|ax+By+C|
d=
	√A2+B2

	|2a*2−2*4−5−4a|
√13=		⇔
	√4a2+4

√13*√4a²+4=13 /² 13(4a²+4)=13*13 /:13 4a²+4=13 4a²=9

	3		3		−5
a=		lub a=−		i b=		−2a
	2		2		2

	3		−5		3		3		−5		−3
y=		x+		−2*		lub y=−		x+		−2*
	2		2		2		2		2		2

	3		−11		−3		1
y=		x+		lub y=		x+
	2		2		2		2

czopo: Dzięki śliczne !

Mila: