| 8 | ||
Kąt α jest ostry i cosα = | ||
| 17 |
| 8 | ||
sin2α + ( | )2 = 1 | |
| 17 |
| 15 | ||
sin2α = | ||
| 17 |
| 15 | 17 | 15 | |||||||||||
tgα = | = | * | = | |||||||||||
| 17 | 8 | 8 |
| 225 | ||
tg2α = | ||
| 64 |
| 225 | 64 | 289 | 17 | |||||
√tg2α+1 = √ | + | = √ | = | |||||
| 64 | 64 | 64 | 8 |
 Maturalne zadanko z zestawu P3, który robię do sprawdzianu.
Maturalne zadanko z zestawu P3, który robię do sprawdzianu.


| 15 | ||
sin2x= | to sinx= √1517 drugie rozwiazanie pomijam | |
| 17 |
| sin2x | 15 | 17 | ||||
tg2x= | = | *( | )2= policz | |||
| cos2x | 17 | 8 |
| sin2x | sin2x + cos2x | 1 | ||||
tg2x + 1 = | + 1 = | = | ||||
| cos2x | cos2x | cos2x |
| 1 | 17 | |||
Czyli √tg2x + 1 = | = | |||
| cosx | 8 |
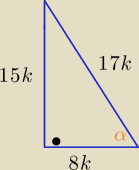 k>0
k>0
| 15 | 225 | |||
tgα= | ⇒ tg2α= | |||
| 8 | 64 |
| 17 | ||
W=.......... = | ||
| 8 |