geometria kamila: mógłby ktoś podpowiedzieć mi jak to obliczyć? Oblicz długość wysokości trójkąta ABC poprowadzonej z wierzchołka B, jeśli A=( − 3, 2), B=( 4, −1), C=(2,5).

Marcin: Wyznaczasz równanie prostej AC. Później liczysz ze wzoru odległość od prostej punktu B.

Alfa: np. skorzystaj ze wzoru na odległość punktu od prostej gdzie: h − szukana odległość B − punkt występujący we wzorze pr. AC − prosta występująca we wzorze zapisana w postaci ogólnej

kamila: dziękuję wysokośc h wyszła mi w przybliżeniu 6,17

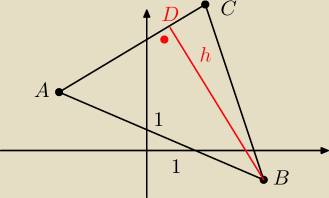
Janek191: h = I BD I A = ( − 3 ; 2) , B = ( 4; − 1) C = ( 2; 5) Prosta AC y = a x + b 2 = −3a + b 5 = 2 a + b −−−−−−−−−−−−− 5 − 2 = 5a 5a = 3 a = 0,6 b = 5 − 2a = 5 − 1,2 = 3,8 y = 0,6 x + 3,8 − postać kierunkowa równania pr AC −−−−−−−−− 0,6 x − y + 3,8 = 0 / * 10 6 x − 10 y + 38 = 0 − postać ogólna pr AC −−−−−−−−−−−−− h obliczymy z wzoru na odległość punktu B od prostej AC :

	I 6*4 − 10*(−1) + 38 I
h =
	√62 + (−10)2

	I 24 + 10 + 38 I		72		72		36
h =		=		=		=
	√36 + 100		√136		2√34		√34

pigor: ..., najlepiej z porównania 2−óch wzorów na pole Δ np. z tw. cosinusów cosα i mamy pole itp. np. |BC|h=36 i |BC|= √34 ⇒ h= 36:√34 ≈ 6,2