`
Agata: Witam, problem z iloczynem kartezjańskim, nie potrafię tego zilustrować na układzie
wspołrzędnych.
Mam coś takiego:
A=[1,3) B={−1,0,3} AxB
21 lut 20:48
Agata: up
21 lut 21:09
MQ: A to odcinek od 1 do 3 jednostronnie domknięty w 1
B to trzy punkty w −1, 0 i 3
AxB to trzy odcinki A na różnych wysokościach B
21 lut 21:25
21 lut 21:50
MQ: Nie
21 lut 21:52
Agata: Ehh, no to nie wiem.
21 lut 21:55
Agata: Może mógłbyś mi podpowiedzieć co jest źle
21 lut 21:58
MQ: A = {x: 1≤x<3}
B = {−1, 0, 3}
AxB = {(x,y): 1≤x<3 i (y=−1 lub y=0 lub y=3)}
Są to trzy odcinki, których wsp. x−owe rozciągają się od 1 włącznie do 3 wyłącznie, a wsp.
y−owe to −1, 0 i 3.
21 lut 22:04
Mila:
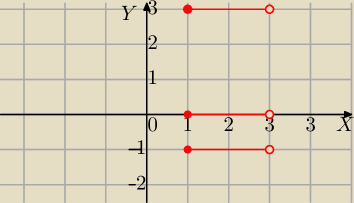
21 lut 22:10
Agata: Ehh nie za bardzo rozumiem ten zapis dlaczego pojawia się ≤. Da się jakoś prościej ?
21 lut 22:12
Agata: A tych punktów nie łączymy pionowo ?
21 lut 22:13
Mila:
Nie. Byłyby wtedy współrzędne y−owe różne od podanych {−1,0,3}
21 lut 22:17
Agata: No ok, tylko teraz kwestia tego, że w zadaniach pojawiają się nawiasy w różnych postaciach
[,(,{
Jak to interpretować, bo niestety muszę to zrozumieć, a jak dostanę inny przykład, to nic nie
wskóram.
21 lut 22:20
Aga1.:
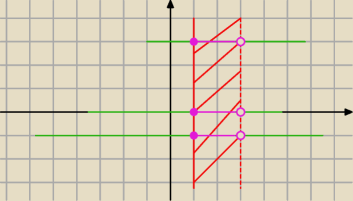
21 lut 22:20
Agata: Oba rozwiązania są dobre, czy jak ?
21 lut 22:23
Aga1.: Na czerwono zaznaczyłam zbiór A, na zielono zbiór B, AxB na różowo
21 lut 22:39
MQ: @Aga1 −− niedokładnie
Na czerwono zaznaczyłaś zbiór (x,y) takich, że x∊A
Na zielono zaznaczyłaś zbiór (x,y) takich, że y∊B
Na różowo zaznaczyłaś część wspólną tych poprzednich, co dało AxB
21 lut 22:44
Agata: MQ; Możesz polecić jakaś dobrą lekturę, która rozjaśni mi trochę umysł na ten temat ?
21 lut 22:49
MQ: Niestety, jedyna dobra lektura na ten temat, jaką znam, to moje zeszyty z liceum do matematyki.
Mieliśmy świetnego profesora.
Poza tym może jedynie "Matematyka w szkole średniej" tłum. z jęz. angielskiego Wojciech
Jędrychowski −− wyśmienite, ale trudne do dostania.
Czasami pojawia się na Allegro za bezcen, albo szukać w antykwariatach.
21 lut 23:16
Agata: Mogłabym wiedzieć(o ile masz pojęcie), w którym tomie znalazłabym iloczyn kartezjański ?
22 lut 01:11
Trivial:
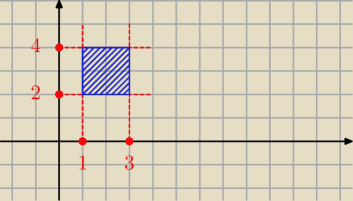Agato, iloczyn kartezjański to nic innego jak pary "każdy z każdym".
{ 1,2,3 } × { 3, 4 } = { (1,3), (1,4), (2,3), (2,4), (3,3), (3, 4) }
Dla ciągłych przedziałów jest to prostokąt.
[1,3]×[2,4] =
rysunek
A dla Twojego zadania jest to:
[1,3)×{−1,0,3} = { (x,y) : x ∊ [1,3), y ∊ {−1,0,3} }
Są to wszystkie pary takie że pierwsza współrzędna może być ze zbioru [1,3), a druga może mieć
3 różne wartości − konkretnie −1, 0, 3.
22 lut 01:19
Trivial: Dobry rysunek ma Mila.
22 lut 01:21
Agata: Dziękuje, tym opisem pozwoliłeś mi zrozumieć istotę tematu. Porobię kilka przykładów i zobaczę
jak to wyjdzie. Mogę wiedzieć, dlaczego rysunek Mili jest poprawny ?
22 lut 01:26
Trivial:
x ∊ [1,3)
y ∊ {−1, 0, 3} czyli y = −1 lub y = 0 lub y = 3.
Pary "każdy z każdym" to:
(x,−1), (x,0), (x,3) gdzie x ∊ [1,3)
Otrzymujemy 3 odcinki tak jak u Mili.
22 lut 01:29
Agata: Ok, dziękuje Ci bardzo
22 lut 01:31
