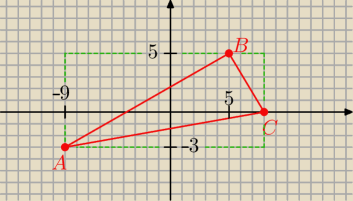
Maturalne Hajtowy: Punkt "C" jest zaznaczony poglądowo, bo ABC ma być prosty a "C" ma leżeć na osi OX. TREŚĆ Punkty A=(−9;−3) i B=(5;5) są wierzchołkami trójkąta prostokątnego ABC, w którym AB jest przeciwprostokątną. Wyznacz współrzędne wierzchołka C wiedząc, że leży on na osi OX Policzyłem sobie prostą AB oraz odległość odcinka |AB| − bo nie wiem wgl co w tym zadaniu zrobić i jak je ruszyć. Nie lubię brył ani geometrii prosta AB: y=ax+b −3=−9a+b 5=5a+b −8=3a

	8		2
a=−		=−2
	3		3

	40		15		40		25
b=5−		=		−		=
	3		3		3		3

	2		1
y=−2		x + 8
	3		3

|AB| = √(5+9)²+(5+3)²=√14²+8²=√260=2√65

Hajtowy: Proszę o najkrótszy i najłatwiejszy sposób na ruszenie tego zadania, bo wgl nie mam zielonego pojęcia jak się za to zabrać.

bezendu: Z twierdzenia pitagorasa skorzytsaj

Hajtowy: AB²=AC²+BC² Ale ja danych tu ni mam

bezendu: Jak to nie masz danych ? Wszystko masz.skoro punkt c leży na osi OX to ma współrzędne (x_c,0) Teraz jasne?

Saizou : z warunku prostopadłości wektorów piszę bez strzałek v=[a:b] i u=[c] v⊥u→a*c+b*d=0

Saizou : oczywiście u=[c: d]

Hajtowy: Fajnie, że jestem w maturalnej klasie a mam zaćmienie mózgu AB²=260 AC² = ... BC² = ...

Hajtowy: Saizou nie umiem wektorów − nie uczono mnie.

bezendu: odcinek AC ma postać: A=(−9,−3) C=(x_c,0) (−9−x_c)²+(−3)² Odcinek BC (5−x_c)²+5²

Saizou : ale wg mnie to jest najkrótsza metoda xd

bezendu: Wyznaczenie równania prostej AB jest zbędne.

Eta: wektory

bezendu: Eta 20:54

Saizou : Eta już sugerowałem wektory xd

Hajtowy: 260 = x_c²+ 18x_c + 81 + 9 + x_c² − 10x_c + 25 + 25 260 = 2x_c² + 8x_c + 140 2x_c² + 8x_c − 120 = 0 x_c = −10 v x_c=6 x_c (−10;0) v x_c(6;0) Dalej nie wiem zbytnio skąd te odcinki AC i BC Ci się wzięły ale policzyłem

Hajtowy: Saizou albo Eta proszę o rozpisanie metodą wektorów − tylko tak jak dla przedszkolaka, może bardziej mi to spasuje niż PITAGORAS

bezendu: To jest długość odcinka,przecież masz wzór w tablicach na długość odcinka ? Ja nic nowego nie wymyśliłem, można jeszcze wersję z okręgiem, ale chyba trudniejsza od tej.

Hajtowy: bezendu ja chyba mam totalne zaćmienie − ale kojarzę o czym mówisz

bezendu: To niech lepiej Ci się rozjaśni zrób sobie wszystkie zadania z zadania.info dotyczące geometrii analitycznej

Saizou : no to liczymy

	=[5+9:5+3]=[14;8]
AB

	=[5−x:5−0]=[5−x:5]
CB

14(5−x)+8*5=0 70−14x+40=0 110=14x

	110
x=
	14

	110
C(		:0)
	14

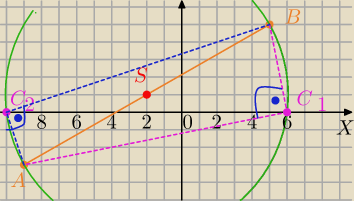
Mila: Punkty A=(−9;−3) i B=(5;5) AB− przeciwprostokątna. 1) Srodek AB: S=(−2,1) |AS|=√7²+4²=√49+16=√65 2) Kreślimy okrąg o promieniu r=√65 i środku S(−2,1) ( geometryczne wyznaczanie, konstrukcje miałeś?) ∡ACB jest prosty jako wpisany w okrąg i oparty na średnicy. (x+2)²+(y−1)²=65 równanie okręgu: Algebraicznie: Na osi x punkty: (x,0) (x+2)²+(0−1)²=65⇔(x+2)²=64 x+2=8 lub x+2=−8 x=6 lub x=−10 C₁(6,0) C₂(−10,0)

Hajtowy: Mila dziękuję za propozycję rozwiązania Nie wpadłbym raczej na taki pomysł

Hajtowy: Saizou coś Ci nie wyszło

Mila: Hajtowy, przecież masz te wiadomości o kącie wpisanym w okrąg.

Saizou : dla: A(−9:−3) B(5:5) C(6:0)

	8		4
aAB=		=
	14		7

	−5
aBC=		=−5
	1

a_AB*A_BC[N≠]]−1 wiec nie są prostopadłe xd

Saizou : ale jestem głupi, nie doczytałem zadanie <głupi ja>

Saizou : poprawię metodę wektorową

	=[x+9:3]
AC

	=[x−5:−5]
BC

(x+9)(x−5)−15=0 x²+4x−45−15=0 x²+4x−60=0 x²+4x+4=64 (x+2)²=64 lx+2l=8 x+2=8 lub x+2=−8 x=6 x=−10

Mila: Saizou Bo ma być prostopadłe: AC⊥BC, i jest. Źle zinterpretowałeś treść− AB to przeciwprostokątna, a prostopadłe są do siebie przyprostokątne.

Saizou : dlatego napisałem <głupi ja> ale już się poprawiłem xd

Mila: Wektorami jest najprościej.Trzeba wiedzieć jak obliczać współrzędne wektorów i iloczyn skalarny.

Saizou : nie wątpię w wektory a w siebie