dziedzina edek676: WYZNACZ DZIEDZINĘ FUNKCJI y = √x−1/(3−x)

Antek:

	x−1
3−x≠0 i		≥0
	3−x

edek676: 3−x≠0 x≠3 D=R−{3} x−1 / 3−x ≥ 0 / *(3−x)² (x−1)*(3−x) ≥0 3x−x²−3+x ≥0 −x² +4x − 3 ≥0 Δ=4 x1=4 x2= 1 xe (−∞;1>u<4;∞)

edek676: ?

Antek: Edek myslisz ? Masz przeciez postac iloczynowa wiec miejszca zerowe juz masz a wyliczyles zle Poza tym dziedzina zle masz wyznaczyc czesc wspolna z tych dwoch warunkow

Antek: taka jest ta postac (x−1)(3−x)≥0 wiex x−1=0 lub 3−x=0

edek676: to x=1 i x=3

edek676: to czesc wspolna to = 3 wiec D=R−{3}

Antek: czyli kiedy (x−1)(3−x)≥0 w jakich przedzialach Poza tym wyznaczyles ze x nie rowna sie 3 wiec napisz dziedzine tej funkcji Tylko napisz czy wiesz albo nie weisz

Antek: 17:37 zle

edek676: to nie wiem

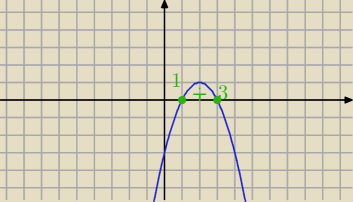
Antek: Widzisz teraz

edek676: D<1;3>

Antek: Na wykresie tej funkcji widzisz ze x∊<1,3> ale z awrunku 3−x≠0 to x≠3 dziedzina tej funkcji bedzie x∊<1,3>\{3} co jest rownoznaczne zapisem x∊<1,3) czy juz teraz wiadomo ?

edek676: tak dzieki!

Antek: Musisz ta trojke wyrzucic z dziedzinny do dla x=3 masz niedozwolone dzielenie przez 0