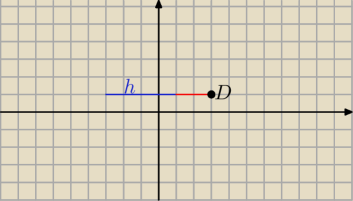
geom analit. jerey: w trojkąt rownoboczny ABC ktorego wierzchołek A=(−3,2) wpisano w okrąg o środku S=(1,2). Oblicz wspołrzędne punktów stycznosci tego okregu z bokami trójkąta ABC z wektorów znalazłem wspołrzędne wierzchołka D SA = [ 1− (−3), 2−2] ⇒ [4,0]

	1
SD=		SA ⇒[2,0]
	2

AD= [6,0] DS = [x−1, y−2]

	1
DS=		[6,0] ⇒ D[3,2]
	3

wiem tez ze przez punkt D przechodzi prosta x=3

jerey: juz znalazłem podobne rozwiazanie na forum. temat do zamkniecia ;

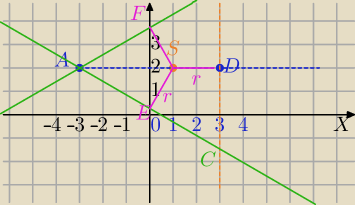
Mila: D=(3,2) jeden z punktów styczności. r=2 SA^→=[−4,0]

	−1
SD→=		SA→=[2,0]
	2

S(1,2)→[2,0]→D(3,2) Prosta AB jest odległa od punktu S o 2 . AB: y=ax+b i 2=−3a+b⇔b=3a+2 AB: y=ax+3a+2⇔ax−y+3a+2

|ax0−y0+3a+2|
	=2 podstawiamy wsp. punktu S
√a2+1

|a−2+3a+2|
	=2⇔|4a|=2√a2+1 /2
√a2+1

16a²=4*(a²+1) 12a²=4

	1
a2=
	3

	√3		√3
a=		lub a=−
	3		3

AB:

	√3
y=		x+√3+2 lub
	3

	√3
AC: y=−		x−√3+2
	3

Pozostaje Ci napisać równania prostopadłych do AB i AC , przechodzących przez S i znaleźc wsp. punktów przecięcia E i F.

jerey: dziekuje

Mila: Dokończyłeś? Napisz wsp. punktów E i F. Może ktoś skorzysta.

jerey: ok, mając rowanie prostej AB i AC, znajdujemy kolejno rownania prostopadłych do prostych AB i AC przechodzących przez S rowanie prostej FS y=−√3x+2+√3 rowanie prostej ES y=√3+2−√3 mamy rownania prostych AB, AC FS ES znajdujemy wspolrzedne punktu E z układu równan:

	√3
y=−		+√3+2
	3

y=√3+2−√3 rozwiązujemy układ ⇒x=0 y =2−√3 analogicznie rozwiązujemy układ szukając współrzędnych punktu F stąd mamy x=0 i y= √3+2

Mila: Opuściłeś x w równaniach prostych, poza tym dobrze.

jerey: ano rzeczywiscie nie wklepałem x'a