Wyznacz:
Matejko: Wyznacz skale i środek jednokładności która okrąg O1 przekształca na okrąg O2
O1:x2+y2+2x−8=0 O2:x2+y2−14x−8y+64=0
S1(−1;0) r=3
S2(7;4) r=1
skale są k=13 i k=−13 jak to policzyc?
21 lut 15:31
Piotr 10: z promieni
r1=r2*IkI
21 lut 15:33
21 lut 15:34
Matejko: wiem patrzyłem na to bezendu i tamto zrobiłem a to mi nie idzie
21 lut 15:35
bezendu:
Piotr już Ci podał wzór więc nic tu po mnie.
21 lut 15:36
Matejko: ale ja wiem jak skale policzyć
i promienie też tylko jak zadanie policzyć o to mi chodzi
21 lut 15:40
bezendu:
x2+y2+2x−8=0
x2+2x+y2−8=0
(x+1)2−1+y2−8=0
(x+1)2+y2=9
S1=(−1,0) r=√9=3
x2+y2−14x−8y+64=0
x2−14x+y2−8y+64=0
(x−7)2−49+(y−4)2−16+64=0
(x−7)2+(y−4)2=1
S2=(7,4) r=1
21 lut 15:45
21 lut 15:50
Mila:
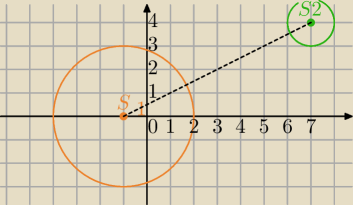
S
1(−1;0) r=3
S
2(7;4) r=1
O1:x
2+y
2+2x−8=0 , O2:x
2+y
2−14x−8y+64=0
| | 1 | |
A (x,y)−środek jednokładności o skali k= |
| |
| | 3 | |
z definicji jednokladności
| | 1 | |
[7−x,4−y]= |
| *[−1−x,0−y] |
| | 3 | |
dalej spróbuj sam
Są też gotowe wzory:
S(a,b) środek jednokladności
k − skala jednokładności
P(x,y)− dany punkt, P'(x',y') −punkt jednokładny
x'=k*(x−a)+a
y'=k(y−b)+b
21 lut 15:57
Matejko: rozumiem dziękuje bardzo a np tu dlaczego k=−1 a nie k=1 np?
O
1:x
2+y
2+6x−6y+14=0
O
2:x
2+y
2−18x+2y=78
21 lut 17:43
Matejko:
21 lut 17:53
Mila:
To są okręgi o różnych promieniach, nie wiem o co pytasz.
21 lut 17:55
Matejko: w tych okręgach co podałem dlaczego jednokładność jest równa −1?
21 lut 18:03
Matejko:
21 lut 18:08
Mila:
(x+3)2−9+(y−3)2−9+14=0⇔(x+3)2+(y−3)2=4 r=2
x2+y2−18x+2y=78 może jest x2+y2−18x+2y+78=0?
21 lut 18:09
Matejko: tak sorki
21 lut 18:24
Mila:
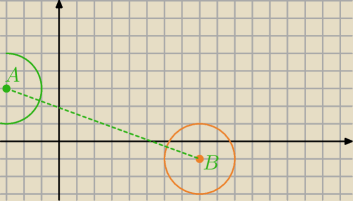
II okrąg
(x−9)
2−81+(y+1)
2−1+78=0
(x−9)
2+(y+1)
2=4
r=2
okręgi są przystającymi figurami, ale znajdują się w innych miejscach.
Skala jednokładności k=1 to oznacza, że figura pozostaje w tym samym miejscu.
Jednokładność o skali k=−1 to jest symetria środkowa.
To należy znaleźć środek symetrii , który leży w środku AB.
21 lut 18:42
Matejko: aha dzięki
21 lut 19:22
Mila:
21 lut 19:44