Czy to zadanie ma rozwiązanie????
maabaa: przekrojem osiowym stożka jest trójkąt prostokątny o polu 25cm2
Oblicz średnice podstawy tego stożka, jeżeli wysokość tego stożka ma długość 10 cm.
21 lut 14:17
J:
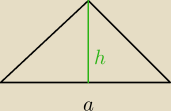
21 lut 14:21
maabaa: 5

i to jest średnica podstawy tego stożka

?
21 lut 14:26
wredulus_pospolitus:
si
21 lut 14:27
J: A co, takie dziwne.. popatrz,że h musi być połową a, ten trójkąt to połowa kwadratu

21 lut 14:29
wredulus_pospolitus:
chociaż chwila chwila ... ktoś niesamowicie skopał to zadanie (chyba że treść źle przepisana)
ponieważ:
b,c −−− przyprostokątne
| | 2500 | |
b2+c2 = 52 −> |
| + c2 − 25 = 0 −> //e=c2 // −> e2 − 25e + 2500 = 0 <−−−− brak |
| | c2 | |
rozwiązań

czyli ... nie istnieje taki trójkąt prostokątny o polu = 25 ... aby jego przeciwprostokątna =10

21 lut 14:31
wredulus_pospolitus:
| | 1 | |
no to J ... skoro h to połowa 'a' to czemu a=5 = |
| |
| | 2 | |
21 lut 14:32
J: h jest połową a (przekątna kwadratu) , zadanie jak piszesz jest "skopane (teraz to widzę)
21 lut 14:35
wredulus_pospolitus:
mnie tknęło jak zobaczyłem że przeciwprostokątna =5 ... wiec mając prostokątny równoramienny
byłby by boki 5
√2,5
√2,5 (i wysokość na przeciwprostokątna 10) aby osiągnąć pole 25 i
zaczęło mnie to intrygować

21 lut 14:38
maabaa: no i właśnie o to pytam... bo treść przepisana "dobrze" ....
21 lut 14:39
wredulus_pospolitus:
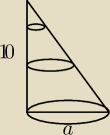
chyba że ... nie jest to 'standardowy' stożek ... rys:
wtedy a=5

i się zgadza wszystko
21 lut 14:42

 i to jest średnica podstawy tego stożka
i to jest średnica podstawy tego stożka ?
?

 czyli ... nie istnieje taki trójkąt prostokątny o polu = 25 ... aby jego przeciwprostokątna =10
czyli ... nie istnieje taki trójkąt prostokątny o polu = 25 ... aby jego przeciwprostokątna =10





 chyba że ... nie jest to 'standardowy' stożek ... rys:
wtedy a=5
chyba że ... nie jest to 'standardowy' stożek ... rys:
wtedy a=5  i się zgadza wszystko
i się zgadza wszystko