definicja rtf: Definicja wielościanu foremnego Wielościanem foremnym nazywamy wielościan wypukły, którego wszystkie ściany są przystającymi wielokątami foremnymi i każdy wierzchołek należy do takiej samej liczby ścian. Interesuje mnie druga część definicji "i każdy wierzchołek należy do takiej samej liczby ścian." Czy istnieje wielościan, którego ściany są przystającymi wielokątami foremnymi zawierający dwa wierzchołki, gdzie liczby ścian przypisane tym wierzchołkom są różne?

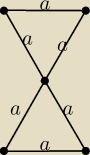
wredulus_pospolitus: oczywiście, np.:

rtf: Wielościan składający się z dwóch ścian? Czy istnieje wielościan wypukły, którego ściany są przystającymi wielokątami foremnymi zawierający dwa wierzchołki, gdzie liczby ścian przypisane tym wierzchołkom są różne?

MQ: No, przecież ci wredulus pokazał.

wredulus_pospolitus: nie ma wielościanu składającego się z dwóch ścian a drugie pytanie −−− mój rysunek prezentuje odpowiedź na to pytanie

wredulus_pospolitus: masz wielościan (dokładnie to 6 ścian ma), każdy długości 'a' ... każda ściana połączona z dwoma wierzchołkami ... a jest wierzchołek który jest połączonych z 4ścianami (podczas gdy pozostałe tylko z dwoma)

rtf: Z całym szacunkiem, ale ja widzę kawałek siatki wielościanu składającego się z dwóch ścian. Być może to głupie, ale nie widzę tego co mam widzieć na tym rysunku.

wredulus_pospolitus: boże ... wielościany a nie wielokąty ... ale to działa tak samo w R³

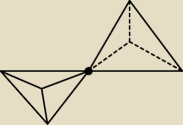
wredulus_pospolitus: powiedzmy, że tutaj wszystkie krawędzie są równe

PW: Mam słabą wyobraźnię przestrzenną, ale spróbuję: Trzy kwadraty są bokami wielościanu, którego podstawy − "górna" i "dolna" są trójkątami równobocznymi. Do tych kwadratów doklejamy "daszki" złożone z czterech trójkątów równobocznych. Powstaje w ten sposób czternastościan o wszystkich ścianach będących trójkątami równobocznymi. Wierzchołki "daszków" należą do czterech ścian, a wierzchołki w podstawie − do pięciu. Sprawdź, bo mogę się mylić (patrz zdanie pierwsze).

PW: wredulusie, Twój nie jest wypukły.

rtf: PW miałeś rację. Wszystko wskazuje na to, że taki wielościan jest wypukły. Dzięki.

wredulus_pospolitus: mhm ... faktycznie ... musiałem chwilkę pomyśleć i przypomnieć sobie definicję wypukłości

PW: Też kombinuję jak koń pod górę. Wystarczyło poszukać analogii z niższego wymiaru, jak mówił wredulus. Sklejenie dwóch trójkątów równobocznych wzdłuż jednego boku nie daje czworokąta foremnego − powstaje romb. Analogia przestrzenna − sklejenie dwóch czworościanów foremnych jedną z płaszczyzn daje wielościan (o sześciu ścianach), który ma żądaną własność − niektóre wierzchołki należą do trzech ścian, a niektóre do czterech.

Mila: Istnieje pięć wielościanów foremnych (z dokładnością do podobieństwa). http://pl.wikipedia.org/wiki/Wielo%C5%9Bcian_foremny