. Piotr 10: Trapez równoramienny o podstawach długości 20cm i 8cm oraz kącie ostrym, którego miara jest równa 50o, obraca się dookoła prostej zawierającej dłuższą podstawę. Oblicz objętość powstałej bryły obrotowej. Mógłby ktoś mi rozjaśnić, jak to obraca się i co z tego powstaje ?

J: Walec, zakończony obustronnie stożkami

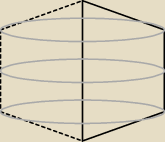
wredulus_pospolitus: w ten oto sposób

J: Przy obliczaniu objętości bryły, daruj sobie oblicznie objętości stozków

wredulus_pospolitus: J ... a to niby czemu ma sobie darować

Ajtek: J, a to dlaczego

wredulus_pospolitus:

	1
J ... Vstożka =		*.....
	3

	2
więc 2Vstożka =		*....
	3

więc musi obliczyć ich objętości

J: Czy objętość powstałej bryły nie będzie równa objetości zielonego walca ?

wredulus_pospolitus: J ... przy polu tak ... przy objętości nie

wredulus_pospolitus:

	2
2Vstożka =		*h*r2
	3

V_{'dodatkowej części walca'} = h*r²

wredulus_pospolitus:

	a−b
gdzie h =
	2

J: OK. Zbłądziłem

Piotr 10: ok zrobilem V_c=12π(tg50⁰*6)² dzięki za pomoc

wredulus_pospolitus: dobrze

Piotr 10: Możesz jeszcze pomoc z jednym zadaniem z wektorami ?

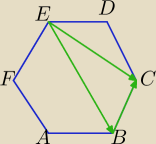
Piotr 10: Dany jest sześciokąt foremny ABCDEF(rysunek obok). Niech u^→=AB^→ oraz w^→=BC^→. Przedstaw wektor EC^→ oraz wektor EB^→ w postaci a*u^→+b*w^→, gdzie a i b są liczbami rzeczywistymi.

Piotr 10: ?

Piotr 10: EB^→=EA^→+AB^→

Piotr 10: Hmm ?

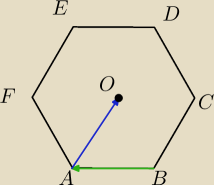
wredulus_pospolitus: jako, ze jest to szcześciokąt foremny to: −AB^→ + BC^→ = BO^→ = −OB^→ należy zauważyć, że: AB^→ = ED^→ oraz DC^→ = OB^→ więc: EC^→ = AB^→ + OB^→ = ....