. Piotr 10: Dane są punkty A=(2;2), B=(5;3). Na prostej o równaniu x+y=0 wyznacz punkt C tak, by długość łamanej ACB była najmniejsza. Jak zrobić obraz punktu A lub B w symetrii wzgledem tej prostej

Piotr 10: Czy A'=(−2;−2) ?

J: Zrób rysunek i zobaczysz,że tym punktem jest punkt (0,0) ( punkt A należy do prostej y = x

Piotr 10: ale jak zrobię obraz punktu A ww symetrii wzgledem prostej x+y=0 , to potem napiszę równanie prostej A'B, następnie znajde punkt wspólny prostej A'B i x+y=0

J: Czy łaman jest ACB ?

Piotr 10: Tak treść dobrze przepisana, głównie kieruje się rozumowaniem z tej strony. Dość podobne zadanie, ale łatwiejsze bo tam była prosta y=4 http://www.zadania.info/8077442

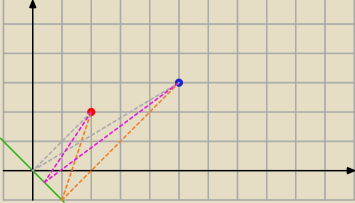
wredulus_pospolitus: J ... a ja bym nie był tego taki pewny fioletowa może okazać sie najbardziej optymalną drogą

Piotr 10: To jak panowie, jak zrobić symetrię tego punktu względem prostej? Czy mój pomysł jest zły i inny próbować wymyslec ?

J: I jest Trzeba zrobić tak, jak w tamtym zadniu. Znależć punkt B^' w symetri osiowej względem prostej y = − x, potem prosta AB^' i jej punk przecięcia z prostą y = −x

Piotr 10: no ja to wiem przecież.. pisałem na początku, nie umiem zrobić symetrii punktu wzgledem tej prostej

J: Punkt B^' bedzie lezał na prostej y = x + b , b wylicz z punktu (5,3).Potem punkt przecięcia prostych y = −x oraz y =x +b ( to będzie środek odcinka BB^' ) i wyznaczysz współrzedne punktu B^'

Piotr 10:

	1		1
Wyszło mi C=(		; −		) jak mógłbyś, to sprawdź
	3		3

Piotr 10: B'=(−3;−5) jak coś

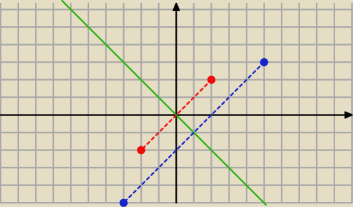
wredulus_pospolitus: graficznie

Piotr 10: thx