rozwiąż
anonim: Jeszcze jeden, a dokladniej 2 problemy
Ctg2x> 3
I
|sinx|>|cosx|
20 lut 22:51
Ajtek:
|sinx|>|cosx| najłatwiej jest rozwiązać graficznie wg mnie.
20 lut 22:58
anonim: A jak z ctg? Tez myślałem nad graficznym rozwiązaniem
20 lut 23:06
Ajtek:
Też najłatwiej
.
20 lut 23:06
anonim: A dla jakiej wart x ctgx=3? To by ulatwilo cale zadanie
20 lut 23:08
Ajtek:
Jak ctgx=3
Ty masz ctg
2x
.
20 lut 23:10
anonim: No tak, ale ctgx> 3 i ctx < −3 a majac x dla ctgx= 3 bede mial x dla ctg x=−3 co by ultwilo
20 lut 23:13
Ajtek:
O masz
Jak rozwiążesz taką nierówność:
a
2>3 zostaw funkcje trygonometryczne w tej chwili w spokoju
.
20 lut 23:14
anonim: Ej chwila, wiem co chcesz udowodnic. Nie 3, a √3 . Pomyliłem się.
20 lut 23:16
Ajtek:
.
20 lut 23:18
Janek191:
ctg2 x > 3 ⇔ ctg x < − √3 lub ctg x > √3
20 lut 23:18
Godzio:
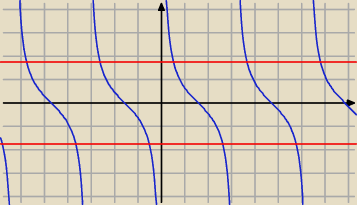
ctg
2x > 3 ⇒ ctgx >
√3 lub ctgx < −
√3
Rozwiązujemy odpowiednie równania, żeby znaleźć punkty przecięcia:
| | π | | π | |
x = |
| + kπ oraz x = − |
| + kπ |
| | 6 | | 6 | |
Rysujemy wykres, proste i odczytujemy rozwiązanie:
| | π | | 5 | |
x ∊ (kπ, |
| + kπ) ∪ ( |
| π + kπ, π + kπ) |
| | 6 | | 6 | |
20 lut 23:20
Ajtek:
Wpadł fachura. Cześć
Godzio .
20 lut 23:21
anonim: Tak, tak juz zrobilem
, ale Dziękuję za dokładny opis
20 lut 23:21
Godzio:
Witam
Wpadł, bo jutro wyjeżdża i chce jeszcze coś zrobić
20 lut 23:22
Ajtek:
A dokąd jedziesz, jeśli można wiedzieć?
20 lut 23:22
anonim: Jak jest fachura to moze pomoze jeszcze z cos2x +cos3x+cos4×+...<1+cosx
20 lut 23:23
Godzio:
Do Zieleńca, na snowboard (ostatnie 3 dni wolnego przed kolejnym semestrem), mam nadzieję, że
pogoda dopisze, bo słyszałem, że ma być za ciepło
20 lut 23:23
Ajtek:
Godzio jedź do Soczi, tam jest tak samo ciepło
. Udanego wyjazdu do Zieleńca
.
20 lut 23:24
Mila:
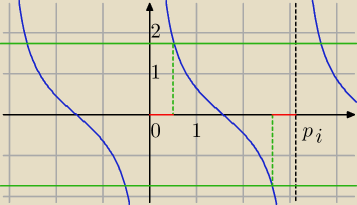
ctg
2x−3>0⇔
(ctgx−
√3)*(ctgx+
√3)>0
ctgx>
√3 lub ctgx<−
√3
| | π | | π | |
0+πk<x< |
| lub |
| +kπ<(x)<π+kπ lub |
| | 6 | | 6 | |
20 lut 23:25
Godzio:
anonim po lewej mamy nieskończony ciąg geometryczny, co trzeba, żeby można było go
wysumować ? (to będzie nasza dziedzina dla x)
No to sumujemy:
| | a1 | |
S = a1 + a2 + ... an + ... = |
| |
| | 1 − q | |
| cos2x | |
| < 1 + cosx wiemy, że cosx < 1 więc 1 − cosx > 0 |
| 1 − cosx | |
cos
2x < (1 + cosx)(1 − cosx) ⇒ cos
2x < 1 − cos
2x ⇒ 2cos
2x − 1 < 0,
pamiętamy przydatny wzorek i otrzymujemy od razu:
cos(2x) < 0
A to już chyba proste
20 lut 23:26
Ajtek:
Mila 
20 lut 23:27
anonim: Dziękuję. Od zawsze trygonometria jest moja pieta Achillesa i nawet taki banal jak wzor na sume
ciągu przy trygonometri wypada mi z glowy
20 lut 23:29