matematykaszkolna.pl
rozwiaz nierówność anonim: Sin2 x <1 Czyli −1 <sin x <1 I odpowiedzią bedzie zbior rzeczywisty bez U {π}{2} czy zle myślę?
20 lut 22:26
anonim:
 π 
Bez
* ?
 2  
20 lut 22:27
Ajtek: Jakie wartości może przyjąć sin2x
20 lut 22:28
ICSP: a okres?
20 lut 22:28
Ajtek: A sorry to jest nierówność . Cześć ICSP emotka.
20 lut 22:29
ICSP: Witam emotka
20 lut 22:29
anonim: <0, 2π>
20 lut 22:29
Antek: ja niedlugo bede miala emotka
20 lut 22:30
anonim:
 π 3π 
Bez
i
?
 2 2 
20 lut 22:31
pw: sinx∊[−1;1] a skoro bez 1 i bez −1 to π/2<x<3π/2
20 lut 22:31
pw: oczywiście pamiętamy że to funkcja okresowa
20 lut 22:32
ICSP:
 π 
x ∊ R \{
+ kπ , k ∊ C }
 2 
20 lut 22:33
anonim: Icsp a nie 2kπ? W koncu π bedzie nalezalo do odp, czy sie myle?
20 lut 22:35
ICSP: sin(π) = 0 < 1 zatem π należy do odp. sin2x < 1 ⇒ sinx ≠ 1 ∧ sinx ≠ −1
20 lut 22:38
anonim: I mam jeszcze pytanie do podobnej nierownoxci a mianowicie Tg2x > 1
20 lut 22:38
anonim: A zrozumialem swoja głupotę ktora pokazalem wam za pomocą poprzedniego komentarza
20 lut 22:39
anonim: Tzn tego z 2kπ
20 lut 22:39
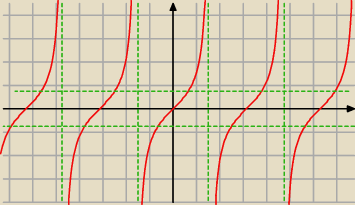
Domel: rysunek No to analogicznie
 π 
D: R/{
+ kπ}
 2 
1 < tgx < −1
 π k π k 
x∊(
+
π ;
+
π) dla k∊C
 4 2 2 2 
20 lut 23:04
Domel: Zaraz − powinno być
 π π π π 
x∊(
+
k ;
+
k)
 4 4 2 4 
20 lut 23:11
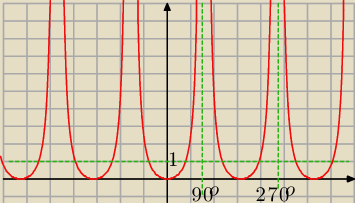
Domel: rysunekwykres f−cji tg2x no się kurde chyba zakałapućkałem bo z wykresu wychodzi
 π π π 3 
x∊(
+ kπ ;
+ kπ) ∨ (
+ kπ ;
π + kπ)
 4 2 2 2 
20 lut 23:24