wielomiany
potrzebujacy:
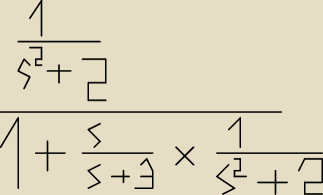
Cześć trochę zardzewiałem z matmy

potrzebuje obliczyć coś takiego (1/(s
2+2))/(1+(s/(s+3))*(1/(s
2+2))
proszę o pomoc mozę być link do podobnego zadanie, ( w części zadaniowej forum sa tylko proste
przyklady

)
20 lut 21:46
potrzebujacy: 52
20 lut 21:48
Trivial:
Pomnóż licznik i mianownik przez (s2+2)(s+3). Pozbędziesz się ułamków piętrowych.
20 lut 21:48
potrzebujacy: coś mi nadal nie pasuje

w wolframie mozna zaobaczyć tylko wynik i nadal sie nie zgadza ( za moich dawnych czasów była
funkcja "step by step " a teraz tylko płatnie

)
możesz to rozwiązać krok po kroku ?
20 lut 21:56
PuRXUTM: | | | |
= |
| =U{(s+3)(s2+2)}{(s2+2)(s+( |
| | | s+(s+3)(s2+2) | |
| | | (s+3)(s2+2) | |
| |
| | s+3 | | s+3 | |
s+3)(s2+2))}= |
| = |
| =no i to chyba wszystko co można |
| | (s+(s+3)(s2+2)) | | s3+3s2+3s+6 | |
zrobić
20 lut 21:59
potrzebujacy: dzięki wielkie

20 lut 22:00
Trivial:
Zależy co masz na myśli poprzez "obliczyć". Wygląda to na jakąś funkcję przenoszenia filtru.
20 lut 22:01
potrzebujacy: potrzebuje to dokladnie do stabilnosci ukladu ( sterowanie )
20 lut 22:05
potrzebujacy: powinno być oczywiscie w formie
= ...( np. s2) / (s6 −+ .... )
to wystarczy
20 lut 22:06
Trivial: Czy do oceny stabilności nie trzeba czasem znać biegunów?
20 lut 22:12
potrzebujacy: a może mi ktoś wytłumaczyć dlaczego mi nie wychodzi jeżeli robię tą metoda ?
http://www.matematykam.pl/zlozone_ulamki.html
wychodzi cos takiego :
1+(s/s+3)*(1/(s
2+2)) * (s
2 +2 / 1)
nastepnie skracam ;
1+(s/s+3)*1
i mam takiki błedny wynik ?
20 lut 22:16
potrzebujacy: *Czy do oceny stabilności nie trzeba czasem znać biegunów?
Chodzi o stabilność układów sterowania ( urządzenie )
20 lut 22:18
Trivial:
Zapisz normalnie, bo nie wiadomo co masz na myśli
| | licznik | |
U{licznik}{mianownik} → |
| |
| | mianownik | |
U jest wielkie i nie ma żadnych spacji między U{ oraz }{.
20 lut 22:19
Trivial:
http://home.agh.edu.pl/~msokol/Stabil.htm
W ujęciu matematycznym warunkiem koniecznym i dostatecznym na to, ażeby układ zamknięty
był stabilny jest, aby pierwiastki równania charakterystycznego (3) miały ujemne części
rzeczywiste. Rozwiązanie tego równania wystarczy, więc dla stwierdzenia czy dany układ liniowy
jest stabilny. Jednak w praktyce ta metoda nie zawsze jest dogodna i wystarczająca.
Bieguny to te pierwiastki równania charakterystycznego.
Widzę, że są też jakieś inne metody.
20 lut 22:23
potrzebujacy: sorry za taki zapis jestem przyzwyczajony do matlaba

a jaka zrobić tą metoda z u ułamek złożony ?
20 lut 22:26
20 lut 22:27
20 lut 22:33
20 lut 22:34
potrzebujacy: co ja pisze za brednie

przeprasza juz wiem gdzei lezy bląd
P.S. bez matmy juz 4 sem. i dalo sie w znaki
dzieki wielkie wszystkim za pomoc

20 lut 22:40
Trivial:
Tak się nie skraca ułamków. Skrócić możesz tylko wtedy, gdy da się wyodrębnić ten sam czynnik z
| | (s+1)(s−3) | | s+1 | |
licznika i mianownika, np.: |
| = |
| . Poza tym ułamek został |
| | (s−3)(s−4) | | s−4 | |
dodatkowo odwrócony i jedynka nie została przez nic pomnożona... Jeśli już to:
20 lut 22:45
Trivial: Sam układ jest stabilny, gdyż każdy biegun ma Re(s) < 0.
20 lut 22:48
potrzebujacy: osobiście używam kryterium Michałowa ( można jedna metoda obliczyć wiekszość zadań

20 lut 22:55
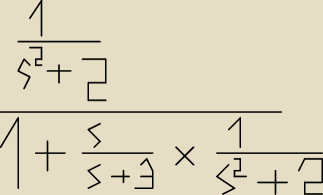 Cześć trochę zardzewiałem z matmy
Cześć trochę zardzewiałem z matmy  potrzebuje obliczyć coś takiego (1/(s2+2))/(1+(s/(s+3))*(1/(s2+2))
proszę o pomoc mozę być link do podobnego zadanie, ( w części zadaniowej forum sa tylko proste
przyklady
potrzebuje obliczyć coś takiego (1/(s2+2))/(1+(s/(s+3))*(1/(s2+2))
proszę o pomoc mozę być link do podobnego zadanie, ( w części zadaniowej forum sa tylko proste
przyklady  )
)
 w wolframie mozna zaobaczyć tylko wynik i nadal sie nie zgadza ( za moich dawnych czasów była
funkcja "step by step " a teraz tylko płatnie
w wolframie mozna zaobaczyć tylko wynik i nadal sie nie zgadza ( za moich dawnych czasów była
funkcja "step by step " a teraz tylko płatnie  )
możesz to rozwiązać krok po kroku ?
)
możesz to rozwiązać krok po kroku ?

 a jaka zrobić tą metoda z u ułamek złożony ?
a jaka zrobić tą metoda z u ułamek złożony ?
 przeprasza juz wiem gdzei lezy bląd
P.S. bez matmy juz 4 sem. i dalo sie w znaki
dzieki wielkie wszystkim za pomoc
przeprasza juz wiem gdzei lezy bląd
P.S. bez matmy juz 4 sem. i dalo sie w znaki
dzieki wielkie wszystkim za pomoc
