wykres funkcji
nikax51: narysuj wykres funkcji
|x
2−4|
f(x)= −−−−−−−
|x|−2
tak naprawde potrzebuje przekształceń do tej funkcji reszte spróbuje sama narysowac

20 lut 21:13
nikax51: proszę o pomoc

20 lut 21:25
Hajtowy: A jak wygląda funkcja |x| ?

20 lut 21:29
Mila:
Z. |x|−2≠0⇔|x|≠2⇔x≠2 i x≠−2
Ustalamy wór funkcji w zależności od znaku wyrażenia pod wartością bezwzględną.
|x
2−4|=x
2−4 dla x
2−4≥0⇔x≤−2 lub x≥2 i x∊D
⇔
|x
2−4|=x
2−4 dla x<−2 lub x>2
|x|=x dla x≥0 i x∊D⇔x∊<0,2)U (2,
∞)
1) x<−2 wtedy mamy wzór funkcji:
| | x2−4 | | (x−2)*(x+2) | |
f(x)= |
| ⇔f(x)= |
| =−(x−2) |
| | −x−2 | | −(x+2) | |
f(x)=−x+2
2) x∊(−2,0)
| | −x2+4 | | (2−x)*(2+x) | |
f(x)= |
| = |
| =−(2−x) |
| | −x−2 | | −(x+2) | |
f(x)=(x−2)
3) x∊<0,2)
| | −x2+4 | | (2−x)*(2+x) | |
f(x)= |
| = |
| =−(x+2) |
| | (x−2) | | x−2 | |
f(x)=−x−2
4) x≥2
f(x)=x+2
20 lut 21:29
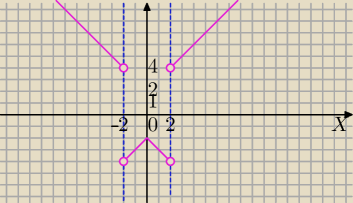
pw: należy określić dziedzinę
Df: x∊R\{−2,2}
później określamy przedziały
(x−2)(x+2) zatem −2 i 2
x zatem 0
mamy 4 przedziały
1) x∊(−∞;−2)
y=[(x−2)(x+2)]/[−(x+2)]=2−x
2) x∊(−2;0)
po przekształceniach y=x−2
3) x∊[0;2)
y=−x−2
4) x∊(2;+∞)
y=x+2
zatem cztery funkcje liniowe
jak dobrze narysujesz to
ZW −4<y≤−2 i y>4
20 lut 21:33
nikax51: dziękuje bardzo

20 lut 21:36



 Z. |x|−2≠0⇔|x|≠2⇔x≠2 i x≠−2
Ustalamy wór funkcji w zależności od znaku wyrażenia pod wartością bezwzględną.
|x2−4|=x2−4 dla x2−4≥0⇔x≤−2 lub x≥2 i x∊D
⇔
|x2−4|=x2−4 dla x<−2 lub x>2
|x|=x dla x≥0 i x∊D⇔x∊<0,2)U (2,∞)
1) x<−2 wtedy mamy wzór funkcji:
Z. |x|−2≠0⇔|x|≠2⇔x≠2 i x≠−2
Ustalamy wór funkcji w zależności od znaku wyrażenia pod wartością bezwzględną.
|x2−4|=x2−4 dla x2−4≥0⇔x≤−2 lub x≥2 i x∊D
⇔
|x2−4|=x2−4 dla x<−2 lub x>2
|x|=x dla x≥0 i x∊D⇔x∊<0,2)U (2,∞)
1) x<−2 wtedy mamy wzór funkcji:
