Równanie kwadratowe z parametrem Radek: Witam mam zadanie. Równanie kwadratowe z parametrem m o różnych znakach (m+1)x²+(2m+1)x+m−1=0 Mógłby mi ktoś powiedzieć co mam źle ? Bo mam problem z interpretacją wyników Zadanie w linku do zdjęcia http://zapodaj.net/images/5f71c7ba0f235.jpg Dziękuje za pomoc

Ajtek: Nie podoba mi się trzecie rozwiązanie.

m−2
	<0
m+1

Radek: (m−2)(m+1) m=2 i m=−1 i co dalej ?

pw: mają być dwa rozwiązania o przeciwnych znakach?

Ajtek: Nanosisz to na wspólną ośkę i część wspólna wszystkich 3 warunków.

pw: warunek 1 − aby były dwa rozwiązania a≠0 zatem m+1≠0 m≠−1 warunek 2 − Δ>0 aby były dwa różne rozwiązania warunek 3 − aby rozwiązania były przeciwnych znaków x1*x2<0 wzory Vietea c/a<0

Radek: tak dwa pierwiastki różnych znaków

pw: a co z trzecim (m−1)(m+1)<0 zatem m∊(−1;1)

Ajtek: pw gdybyś zerknął w link, to byś wiedział z czym jest problem. Warunki kolega Radek doskonale zna.

Aga1.:

	c		m−1
x1*x2<0⇔		<0⇔		<0
	a		m+1

Ajtek: Cześć Aga1. . c=m−2, źle zapisał tutaj, w linku jest wszystko jasne .

pw: no ta mamy m≠−1 m∊(−1;1) i dołączyć należy wyliczenie z delty

Aga1.: Witaj Ajtek, nie czytałam.

Radek: Tak ma być ?

pw: c=m−2 no to (m−2)(m+1)<0 m∊(−1;2)

pw: z delty warunek m>−9/8 ostatecznie pozostanie m∊(−1;2)

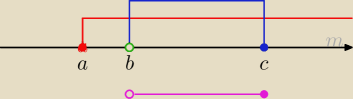
Ajtek: a=−9/8 b=−1 c=2 Na czerwono Δ>0 Zielone kółko m=−1

	c
Na niebiesko		<0
	a

Na różowo, część wspólna wszystkich warunków → Twoje rozwiązanie

Ajtek: Oczywiście w c kółeczko powinno być niezamalowane .

pw: tylko że niebieski przedział jest obustronnie otwarty

Ajtek: Jak widzisz, jest już komentarz odnośnie tego.

Radek: Oki dzięki rozumiem, a mam jeszcze że dwa pierwiastku ujemne x²+3x−4+m=0 Dobrze rozwiązane ? http://zapodaj.net/images/b46b98308ece8.jpg

Ajtek: Wygląda okej .

Radek: Czyli jednak nie aż takie trudne, tylko można się pomylić rysując to wszystko na osi i w odczytaniu prawidłowego rozwiązania

Ajtek: Jeszcze jedna uwaga. Jak masz coś takiego jak u Ciebie w warunku nr 4: wynik wychodzi −3<0 nie zaznaczaj tego na osi .

Radek: Rozumiem obojętnie jaka to by była liczba czy 5<0 czy tez 5>0?

Ajtek: Jeżeli 5<0 to jest jakiś błąd, czyż nie

Radek: No niby jest bo 5 nie jest mniejsze od zera

Ajtek: No właśnie. Takie coś nigdy nie powinno się pojawić, tzn sprzeczność w tego typu zadaniach (niezależne od m)

Radek: No ale chyba jakiś to taki błąd nie jest na które punkty lecą ?

Ajtek: Nie . Chodzi mi tylko o to, żebyś nie zaciemnił sobie obrazu rozwiązania. Na osi zaznaczasz tylko istotne dla rozwiązania warunki z parametrem (m, k, mogą być różne, np jeszcze p)

Radek: 2x²+x+4−6m i rozwiązania dwa maja być ujemne. http://zapodaj.net/images/ecc5ec3cedff6.jpg me(−niesk;²₃>