równanie kwdratowe paulinka123: rozwiąż równanie |x²+ 3x + 2|= |x+1|

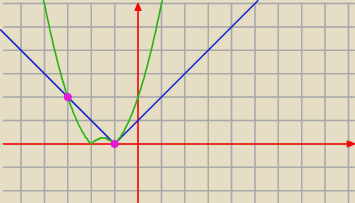
bezendu: (x,y)=(−3,2) lub (−1,0)

paulinka123: i to już jest całe rozwiązanie?

bezendu: A co jeszcze chcesz ?

paulinka123: jakieś krótkie..

bezendu: Skoro za krótkie to nie przepisuj...

Aga1.: Lub tak x²+3x+2=x+1 lub x²+3x+2=−x−1 Ale trzeba liczyć

PW: Chcesz "porządnie wyliczyć", bo rysunek bezendu Cie nie przekonuje? x²+3x+2 = (x+1)(x+2), a więc mamy równanie |(x+1)(x+2)| = x+1. Dla x=−1 otrzymamy zdanie prawdziwe 0=0, a więc liczba −1 jest rozwiązaniem. Dla pozostałych x mamy równanie

	|x+1|
		|x+2| = 1.
	x+1

Ten ułamek po lewej stronie jest równy 1 albo −1, zależy od tego czy x > −1, czy też x < −1. Pobaw się tak, będzie dobrze − dwa równania na dwóch przedziałach (jedno jest zawsze fałszywe, co od razu widać).

PW: O, paulinko, jest jeszcze lepiej − zgubiłem wartość bezwzględną po prawej stronie, równanie ma postać

	|x+1|
		||x+2| = 1, x∊R\{−1}
	|x+1

− tylko udzielając odpowiedzi nie zapomnieć, że −1 też jest rozwiązaniem.

pigor: ..., lub ... nie widzę takiego : |x²+3x+2|= |x+1| ⇔ |(x+1}{x+2}|=|x+1| ⇔ |x+1||x+2|−}x+1}=0 ⇔ ⇔ |x+1|(|x+2|−1)= 0 ⇔ x+1=0 v |x+2|=1 ⇔ x=−1 v x+2=−1 v x+2=1 ⇔ ⇔ x=−1 v x=−3 ⇔ x∊{−1,−3} , gdzie −1 pierwiastek podwójny. ...