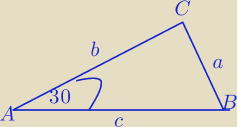
ccc ccc: Miara jednego z kątów trójkąta jest równa 30 stopni. Pole tego trójkąta wynosi p[3}, a promień okręgu opisanego na nim jest równy 2. Oblicz promień okręgu wpisanego w ten trójkąt.

ccc: pole √3 miało tam być

ccc: pomoże ktoś?

ccc: ?

Mila:

	a+b+c
PΔ=		*r
	2

	1
P=√3⇔		*b*c*sin30=√3
	2

b*c=4√3 Z tw, sinusów

a		1
	=2R⇔a=2*2*		=2
sin30		2

Z tw. cosinusów a²=c²+b²−2bc*cos30⇔

	√3
22=c2+b2−2*4√3*
	2

4=c²+b²−12 c²+b²=16⇔(c+b)²−2cb=16 b*c=4√3 (c+b)²−2*4√3=16 (c+b)²=16+8√3 (c+b)²=4*(4+2√3=4*(1+√3)² c+b=2(1+√3)=2+2√3 a+b+c=2+2+2√3

	4+2√3
√3=		*r
	2

	√3
r=
	2+√3

	√3		2−√3
r=		*
	2+√3		2−√3

r=√3*(2−√3}{4−3} r=2√3−3

Mila: w przedostatniej linijce:

	√3*(2−√3)
r=
	4−3

55: αγΩΩ∫∫∫→→→→