wielomiany pomocy bogusia: Pierwiastkami wielomianu czwartego stopnia W(x) są liczby a, b, c, d, które w podanej kolejności tworzą ciąg arytmetyczny o różnicy 2. Suma pierwiastków wielomianu jest równa 8. a) Oblicz pierwiastki a,b,c,d, wielomianu W(x) b) Wiedząc, że dla argumentu 0 wielomian przyjmuje wartości (−15), przedstaw wielomian w postaci W(x) = a₄x⁴ + a₃x³+ a₂x² + a₁x + a₀

bogusia: moze ktos pomoze

Eta: OK Napisałam to rozwiązanie już 3godz. ( strona nie chodziła ) i nie mogłam wysłać! a , b= a+2 c= a+4 d=a+6 bo r= 2 więc: a+b+c+d=8 => 4a +12=8 => a = −1 to b= −1+2= 1 c = −1+4= 3 d= −1+6 =5 b) W(0)= −15 to W(x) =( x +1)(x −1)( x−3)(x −5) = ( x²−1)( x²−8x +15) W(x) = ....... wykonaj mnożenie , zredukuj wyrazy i podaj wynik: PS: Witaj Jakubie Co się stało? ,że forum "zamilkło" ?

Jakub: Witaj Eta! Strasznie jestem na siebie zły, że tego nie zauważyłem. Tym razem to była moja wina. Już jedną rzecz poprawiłem. W przyszłości powinno być lepiej.

Eta: Dzięki Najgorsze ,że nie miałam co ze sobą zrobić przez tak długi czas bez forum to dla mnie ( myślę ,że to już "uzależnienie "

bogusia: dzięki wielkei ja tez nic nie mogłam zrobić ani wysłać ani przeczytać

bogusia: Liczby log3(x−3), log34x, log3x2 , w podanej kolejności tworzą ciąg arytmetyczny. Wyznacz x.

bogusia: Liczby log₃(x−3), log₃4x, log₃x² , w podanej kolejności tworzą ciąg arytmetyczny. Wyznacz x.

bogusia: to W(x) =( x +1)(x −1)( x−3)(x −5) = ( x²−1)( x²−8x +15) = x⁴−8x³+15x²−x²+8x−15= x⁴−8x³+14x²+8x−15

kaz: 2log₃4x=log₃(x−3)+log₃x² rozwiąż równanie

bogusia: czy dobrze policzyłam wielomian

bogusia: i czy mozna zostawic w takiej formie

bogusia: a z jakiego wzoru muszę skorzystać a by rozwiązać to równanie 2log₃4x=log₃(x−3)+log₃x²

bogusia:

bogusia:

Zbronek: wzór na logarytm potęgi i wzór na logarytm iloczynu

Keshia: Eto! proszę o pomoc

Keshia: https://matematykaszkolna.pl/forum/23905.html <−− help

bogusia: pomożecie to równanie rozwiązać nic mi nie idzie 2log₃4x=log₃(x−3)+log₃x²

bogusia: i nawet nie wiem skąd się wzięła ta 2 na przodzie tego logarytmu

bogusia: to W(x) =( x +1)(x −1)( x−3)(x −5) = ( x²−1)( x²−8x +15) = x⁴−8x³+15x²−x²+8x−15= x⁴−8x³+14x²+8x−15 i jeszcze ten nieszczęsny wielomian

Eta: Załozenie: 4x>0 i x −3 >0 => x >3 log₃ 16x² = log₃(x−3)*x² to: (x −3)*x² = 16x² x³ −3x² −16x²=0 x³ −19x² =0 x²( x −19)=0 => x =0 v x = 19 x =0 −−− odzrzucamy ,bonie spełnia założ. odp: x = 19

bogusia: (c(dzięki wielki)) a co do tego wielomianu to pewnie nie można go tak zostawać

Eta: Tak właśnie należy go zostawić

bogusia: rozwiąż równanie 5³*5⁵*5⁷*5⁹*.....5²ⁿ⁺¹ =( ³√5)^{(n2−6)(3n+6)}, n∊N

bogusia: po pierwiastku to co w nawiasie to n²−6

bogusia: możne to mi pomożecie

bogusia: tak ciężko teraz cos wysłać a;no przeczytac ze mi nic nie chodzi

bogusia: rozwiąż równanie 5³*5⁵*5⁷*5⁹*.....5²ⁿ⁺¹ =( ³√5)^{(n2−6)(3n+6)}, n∊N

bogusia: po pierwiastku to co w nawiasie to (n²−6 )

bogusia: tak teraz ciężko się połączyć tym forum

bogusia:

bogusia:

bogusia:

bogusia: pomożecie

Eta: Pewnie ,że pomogę

Eta: aⁿ*a^m = a^n+m więc L= 5^{3 +5+7+.... + 2n+1} wykładnik jest sumą wszystkich liczb nieparzystych

	a1+ an		3 +2n+1		2n+4
Sn=		*n =		*n =		*n=(n+2)*n
	2		2		2

więc L= 5^(n+2)*n teraz prawa strona: ³√5= 5^1/3 więc P=( (5)^1/3)^{(n2−6)(3n+6)}= 5^{(n2−6)(n+2)} zatem: porównując wykładniki otrzymasz: (n+2)*n = ( n²−6)( n+2) /: ( n+2) ,bo n€N n= n² −6 => n² −n −6=0 policz deltę i podaj n pamiętając ,że n€N odp: n = 3

bogusia: czy z takiego wzoru Δ = b² − 4ac

Ergo: Eto zagladniesz tu https://matematykaszkolna.pl/forum/23826.html chodzi tylko o sprawdzenie ukladu rownan. Bylbym wdzieczny

Eta: No to już Bogusiu ( takiego ptyania na tym forum jeszcze nie było! jesteś pierwsza Każdy to wie Δ= 25 √Δ= 5 n₁ = 3 v n₂ = −2 −−−− odrzucamy bo nie jest liczbą naturalną

bogusia: wielkie dzięki wiem ze wam zawracam głowę

bogusia: O wielomianie stopnia trzeciego wiadomo, że ma dwa pierwiastki x₁ = 1 oraz x₂ = −3, przy czym pierwiastek x₂ jest dwukrotny. Wielomian ten dla argumentu (−2) osiąga wartość 6. a) Wyznacz współczynniki tego wielomianu b) Rozwiąż nierówność W(x) ≤ 0

bogusia: W(x) = x (x−3)(x−3)

bogusia: O wielomianie stopnia trzeciego wiadomo, że ma dwa pierwiastki x₁ = 1 oraz x₂ = −3, przy czym pierwiastek x₂ jest dwukrotny. Wielomian ten dla argumentu (−2) osiąga wartość 6. a) Wyznacz współczynniki tego wielomianu b) Rozwiąż nierówność W(x) ≤ 0

bogusia:

bogusia:

bogusia:

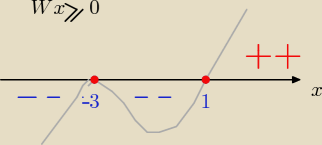
Eta: Och Bogusia , co ja się mam z Tobą 1) W(x) = a*( x −1)(x +3)² bo −3 −−− pierw. dwukrotny W( −2)= 6 więc W( −2) = a *( −2−1)( −2 +3) = a*(−3)* 1 = −3a to −3a = 6 => a = −2 więc W(x) = −2( x −1)(x+3)² = −2x³ −10x² −6x +18 ( wykonaj działania i taki wynik otrzymasz: więc współczynniki są: −2 , −10 , −6 , 18 2/ W(x) ≤0 −2( x −1)(x +3)² ≤0 /*( −2) ( zmieniamy zwrot nierówności , pamiętaj (x−1)(x+3) ≥ 0 rysynek masz więc łatwo odczytać rozwiazanie odp: x€ ( < 1, +∞) U {−3}

Eta: poprawiam chochlika x€<1, +∞) U {−3}

miła: ∫10 + ∫2/ ∫5+1jest równe