rowanie Jacek: bardzo proste mam pytanie do prostej rzeczy mam rozwiazac rownanie tgx + ctgx − 4sin2x = 0 i doszedlem do postaci 1 −−−−−−− − 8sinxcosx = 0 sinx cosx macie pomysly jak to dalej rozwiazac

Jacek:

R: 1 − 8sin²xcos²x = 0

	1
sin2xcos2x −		= 0
	8

	1
sin2x[1 − sin2x] −		= 0
	8

	1
sin2x − sin4x −		= 0
	8

c=sin²x

Jacek: oo dzieki bo sie i si emecze zapisalem tyle kartek ale dzieki wielkie

R: Pamietaj o dziedzinie.

PW: Jacek, byłeś bardzo blisko. Wystarczyło skojarzyć, że 2sinxcosx = sin2x i rozwiązałbyś szybciej niż R.

Bizon: a chociażby tak (1−√2sin2α)(1+√2sin2α)=0

Jacek: dzięki dzięki a ktorys z was bylby sklonny mi pomoc w tozsamosciostatniej bo mi zostala ostatnia bo jutro pisze poprawe z trygonometri a poandto mam pd wszystko sam rozwiazlem izostala mi ostatnia tozsamosc

Jacek: no tak PW bo ja probowalem z sin2x ale zrobilem blad rachunkowy teraz widze −.− ehh no nic ale i tak dzieki

Domel: tgx + ctgx − 4sin2x = 0

	π
D: x ≠ 0 + kπ ⋁ x ≠		+ kπ dla k∊C
	2

sinx		cosx
	+		− 8sinx*cosx = 0
cosx		sinx

sin2x + cos2x
	− 8sinx*cosx = 0
sinx*cosx

sin2x + cos2x − 8sin2x*cos2x
	= 0 => 1 − 8sin2x*cos2x = 0
sinx*cosx

1 − 2*4*sin²x*cos²x = 0 => 1 − 2*sin²2x = 0 (1 − √2sin2x) * (1 + √2sin2x) = 0 1 − √2sin2x = 0 ∨ 1 + √2sin2x = 0

	√2		√2
sin2x =		∨ sin2x = −
	2		2

	π		3		π		5
2x =		+ 2kπ ∨ 2x =		π + 2kπ ∨ 2x = −		+ 2kπ ∨ 2x =		π + 2kπ
	4		4		4		4

	π		7		π		9
x =		+ 2kπ ∨ x =		π + 2kπ ∨ x = −		+ 2kπ ∨ x =		π + 2kπ
	8		8		8		8

Bogdan: po określeniu założeń:

sinx		cosx		2
	+		= 4sin2x ⇒		= 4sin2x ⇒ 4sin2x = 2
cosx		sinx		2sinx cosx

	2		√2		−√2
sin22x =		⇒ sin2x =		lub sin2x =		itd.
	4		2		2

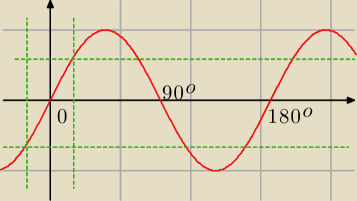Domel: Mam jeszcze pytanie − chyba wyżej na końcu przekombinowałem Czy wyniki nie powinny wyglądać następująco?

	π		π		3		5
x = −		+ kπ ∨ x =		+ kπ ∨ x =		π + kπ ∨ x =		π + kπ
	8		8		8		8

Sorki − po ponad 20 latach matematycznego niebytu zdarzają mi się resety

wredulus_pospolitus: wersja z 10:16 poprawna (poprawiłeś okres) natomiast można zapisać to krócej zauważając, że:

π		kπ		5π
	+		=		+ kπ
8		2		8

więc zapisujesz to jako:

	π		kπ		π		kπ
x=−		+		⋁ x =		+
	8		2		8		2