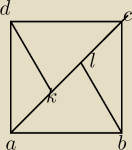
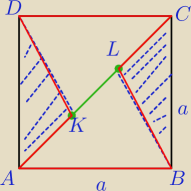
 W kwadracie ABCD wybrano na przekątnej punkty K i L takie, że |AK|=|KL|=|LC|.
Uzasadnij, że pole sześciokąta ABLCDK jest cztery razy większe od pola trójkąta ADK
W kwadracie ABCD wybrano na przekątnej punkty K i L takie, że |AK|=|KL|=|LC|.
Uzasadnij, że pole sześciokąta ABLCDK jest cztery razy większe od pola trójkąta ADK

 o− pole trójkata
widać, że wszystkie maja takie samo pole, bo:
a) podstawa ma taka sama długość
b) wysokość tez ma taka sama długośc
o− pole trójkata
widać, że wszystkie maja takie samo pole, bo:
a) podstawa ma taka sama długość
b) wysokość tez ma taka sama długośc
| 1 | 1 | 1 | 1 | |||||
PΔCLB=PΔAKD= | PΔABC= | * | a2= | a2 | ||||
| 3 | 3 | 2 | 6 |
| 1 | 1 | 2 | ||||
Psześciokata=a2−2* | a2=a2− | a2= | a2 | |||
| 6 | 3 | 3 |
| 2 | 1 | 2 | 6 | ||||
a2: | a2= | * | =4 | ||||
| 3 | 6 | 3 | 1 |