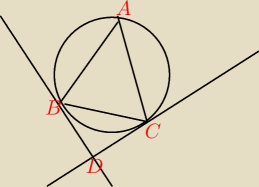
trójkąt ostrokątny trójkąt: Trójkąt ostrokątny równoramienny ABC, (I∡BI = I∡CI), wpisano w okrąg. Nastepnie przez punkty B i C poprowadzono styczne do okręgu przecinające się w punkcie D. Miara kata CDB jest dwa razy mniejsza od miary kąta przy podstawie trójkąta ABC. Oblicz miarę kąta BAC.. co tu dalej można zrobić? rysunek w porządku chyba..

J: Może tak: Skoro I∡CBAI = 2*ICDBI , to I∡BACI = 180^o − 4*ICDBI

pigor: ..., niech |∡BAC|= x= ? , O − środek okręgu, to |∡BOC|= 2x i jeśli 2α − miary kątów przy podstawie ΔBCA, to z warunków zadania masz np. układ równań: 2α+2α+x= 180^o − ΔBAC i 2x+α= 180^o − z czworokąta BDCO ⇔ ⇔ 2x+α= 4α+x ⇔ x=3α − szukana miara kąta BAC. ...

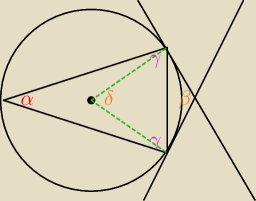
wredulus_pospolitus: δ = 180−β

	1		β
α =		δ (kąty oparte na tym samym łuku) = 90 −
	2		2

z treści zadania wiemy, że γ = 2β stąd:

	γ
α = 90 −
	4

a więc: α+γ+γ = 180 (suma kątów w trójkącie)

	7
90 +		γ = 180
	4

	360
γ =
	7

	540
α =
	7

trójkąt: dziękuję, trochę mnie olśniło