Planimetria Matma: W trójkącie ABC przez wierzchołek A środek O środkowej BD poprowadzono prostą przecinającą bok BC w punkcie L. Wyznacz |CL| i |BL|, jeżeli |BC|=a.

Eta:

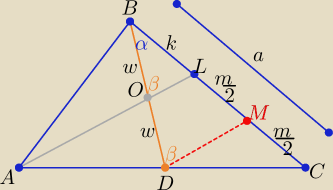
	m
Dorysuj odcinek DM łączący środki boków trójkąta ACL to |CM|=|ML|=		i |BL|=k
	2

|OD|=|OB|=w i DM II AL zatem z tw. Talesa

w		w
	=		⇒k=0,5m
k		0,5m

	1		2
to: |BC|=a= 3k ⇒ |BL|= k=		a , |CL|=2k=		a
	3		3

Eta: I co Matma ? zatkało ?

Matma: Dzięki wielkie

Eta:

Matma: