???: W trójkącie ABC połączono środki D,E,F boków. Wykaż, że pole trójkąta DEF jest cztery razy mniejsze od pola trójkąta ABC. Teoretycznie wiem o co chodzi, ale nie mam pojęcia jak to wykazać w obliczeniach.

	P1
Domyślam się, ze można użyć tego wzoru		=k2 ale znowu nie wiem jak żeby to było
	P2

poprawnie

pigor: ..., a spróbuj może z tw. o odcinku łączącym środki kolejnych boków Δ , oraz z własności boków i przekątnych ... równoległoboków w tym Δ

???: tylko własnie nie wiem jak to zapisać bo teoretycznie to rozumiem, a jakoś wykazać trzeba

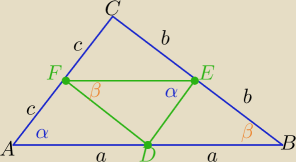
Eta: trójkąt ABC podobny do trójkąta DEF w skali k=2 to:

	P(ABC)
		= k2=4 ⇒ P(ABC)=4*P(DEF)
	P(DEF)

czyli P(DEF) jest 4 razy mniejsze od P(ABC) c.n.u

???: dzięki