Rozwiąż nierówność
Iza: a) |x−2|−|x|<4
b) ||x+1|−x|≤2
Robie w tych przykładach jakieś (pewnie znów śmieszne) błędy i wyniki mam w połowie dobre

17 lut 20:13
Marcin: Napisz jak to liczysz

17 lut 20:15
Iza: ok już

a) x−2=0
x=2
x=0
1. x∊(−
∞,0)
−x+2+x<4
2<4 −> sprz.
2. dla x∊<0,2)
−x+2−x<4
x>1
3. dla x∊ <2,
∞)
x−2−x<4
−2<4 −> sprz.
I oczywiście ja wynik pierwszy i ostatni pominęłam, i napisałam, że x∊(1,
∞)
Poprawny wynik to x∊R
i jeśłi dobrze myślę, to wziął się on stąd że zarówno w 1, jak i 2. wyszły wyniki prawdziwe (
−2<4,)
17 lut 20:20
Marcin: 4>2 to nie jest sprzeczność Izo

17 lut 20:23
Iza: b) |x+1|−x≤2 oraz |x+1|−x≥−2
|x+1|≤2+x |x+1|≥x−2
x+1 ≤ 2+x x+1≥ −2−x x+1≥x−2 x+1≤−x+2
1≤2 x≥−3/2 1≥−2 x≥1/2
x∊<−3/2, 1/2>
a powinno być że x∊<−3/2, +∞)
17 lut 20:25
Iza: no przepisując to tutaj, jeśłi zauważyłeś sama zauważyłam ten błąd, więc pierwszy przykład ok,
z głowy, a drugi, dlaczego 1/2 nie?
17 lut 20:25
Marcin: A to przepraszam

Trzeba było usunąć to "sprz"

17 lut 20:29
Iza: taaak, wiem...ale to dopiero na samym końcu wywnioskowałam.
a jak z drugim przykładem?
Dlaczego zazwyczaj te trudniejsze zadania rozwiązuje poprawnie a w prostszych robię mase
błędów?

17 lut 20:32
Iza: ?
17 lut 20:50
Marcin: Nie było mnie przez jakiś czas. Poradziłaś sobie?

17 lut 21:57
Kozaczek: Iza, musisz jeszcze dla każdego przypadku podać przedziały dla których to liczysz (x∊...) i
wtedy zsumować zbiory

17 lut 22:11
Domel: Dot. zad. 1
1. dla x∊(−∞;0)
2<4 − czyli prawda dla wszystkich x w założonym przedziale
2. dla x∊<0;2)
x>−1 czyli x znowu mieści się w założonym przedziale
3. dla x∊<2;∞)
−2<4 − czyli prawda dla wszystkich x w założonym przedziale
Więc rozwiązaniem są x należące do wszystkich założonych przedziałów a więc x∊R
17 lut 22:31
Domel:
||x+1|−x|≤2
dla x∊(−∞;−1) => |x+1| = −x−1
|−x−1−x|≤2
|−2x−1|≤2
dla x∊(−∞;−1) => |−2x−1| = −2x−1
−2x−1≤2
−2x≤3
dla x∊<−1;+∞) => |x+1| = x+1
|x+1−x|≤2
|1|≤2
1≤2 −> prawda w całym przedziale czyli
x∊<−1;+∞)
ZZ obu przedziałów wynika, że
x∊<−1,5;+∞)
17 lut 22:55
Domel:
W pierwszej części zadania nie rozpatrywałem
x∊<−1;+∞)
bo było to poza przedziałem głównym
x∊(−∞;−1)
17 lut 22:59
Aga1.:
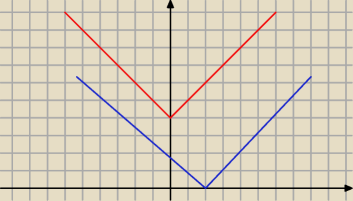
a) Można zrobić graficznie
Ix−2I<IxI+4 ( niebieski jest pod czerwonym ) dla x∊R
18 lut 10:00
Aga1.:
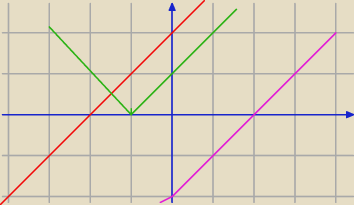
b) graficznie tak
1) Ix+1I≥x+2 Zielony pod czerwonym dla x∊<−1,5;
∞) i
2) Ix+1I≥x−2 (zielony nad różowym) dla x∊R
Ponieważ jest spójnik i to wyznaczamy część wspólną rozwiązań.
i odp.
x∊<−1,5;
∞)
18 lut 10:16


 a) x−2=0
x=2
x=0
1. x∊(−∞,0)
−x+2+x<4
2<4 −> sprz.
2. dla x∊<0,2)
−x+2−x<4
x>1
3. dla x∊ <2, ∞)
x−2−x<4
−2<4 −> sprz.
I oczywiście ja wynik pierwszy i ostatni pominęłam, i napisałam, że x∊(1, ∞)
Poprawny wynik to x∊R
i jeśłi dobrze myślę, to wziął się on stąd że zarówno w 1, jak i 2. wyszły wyniki prawdziwe (
−2<4,)
a) x−2=0
x=2
x=0
1. x∊(−∞,0)
−x+2+x<4
2<4 −> sprz.
2. dla x∊<0,2)
−x+2−x<4
x>1
3. dla x∊ <2, ∞)
x−2−x<4
−2<4 −> sprz.
I oczywiście ja wynik pierwszy i ostatni pominęłam, i napisałam, że x∊(1, ∞)
Poprawny wynik to x∊R
i jeśłi dobrze myślę, to wziął się on stąd że zarówno w 1, jak i 2. wyszły wyniki prawdziwe (
−2<4,)

 Trzeba było usunąć to "sprz"
Trzeba było usunąć to "sprz" 



 a) Można zrobić graficznie
Ix−2I<IxI+4 ( niebieski jest pod czerwonym ) dla x∊R
a) Można zrobić graficznie
Ix−2I<IxI+4 ( niebieski jest pod czerwonym ) dla x∊R
 b) graficznie tak
1) Ix+1I≥x+2 Zielony pod czerwonym dla x∊<−1,5;∞) i
2) Ix+1I≥x−2 (zielony nad różowym) dla x∊R
Ponieważ jest spójnik i to wyznaczamy część wspólną rozwiązań.
i odp.
x∊<−1,5;∞)
b) graficznie tak
1) Ix+1I≥x+2 Zielony pod czerwonym dla x∊<−1,5;∞) i
2) Ix+1I≥x−2 (zielony nad różowym) dla x∊R
Ponieważ jest spójnik i to wyznaczamy część wspólną rozwiązań.
i odp.
x∊<−1,5;∞)