Marcin: |k−1|−|k+3|≥0 |k−1|≥|k+3| /^ k²−2k+1≥k²+6k+9 −8k≥8 k≤−1 Można to tak rozwiązać czy muszę jechać przedziałami?

Godzio: Można. Na takie zadanie fajnie też spojrzeć geometrycznie. Odległość od 1 jest większa lub równa niż odległość od −3.

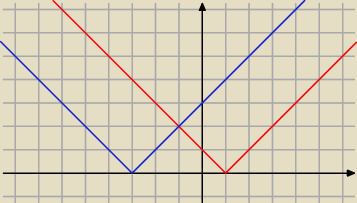
Saizou : można, jest to jak najbardziej poprawne nawet graficznie można czerwony lx−1l niebieski lx+3l i teraz kiedy czerwony jest wyżej niż niebieski →k≤−1

Marcin: Dzięki wielkie Godzio Można sobie trochę czasu dzięki temu zaoszczędzić. Bo przedziały są niefajne

Godzio: Przy takich przejściach, musisz zawsze ustalić, czy przejścia są równoważne, tzn. czy z |k−1| ≥ |k+3| /² ⇒ (k − 1)² ≥ (k + 3)² i czy (k − 1)² ≥ (k + 3)² /√ ⇒ |k−1| ≥ |k+3|

Marcin: Ale typowo graficznie na maturze nie będę przecież rozwiązywać Dzięki Panowie, chciałem się upewnić