nierownosc
alexander: Rozwiązaniem nierównosci x√2≥2x +6 jest:
17 lut 13:50
Hajtowy: Wszystko na jedną stronę.
17 lut 13:53
J: Przenieś wyrazenia z niewiadomą na lewą stronę,wyłącz przed nawias i licz.
17 lut 13:53
alexander: 2x+6 − x√2≥0 ?
17 lut 13:57
alexander: to tak będzie

nie jestem pewny na 100%
17 lut 13:59
J: | | 6 | | 6*(√2+2) | |
x√2 − 2x ≥ 6 ⇔ x(√2 − 2) ≥ 6 ⇔ x ≤ |
| ⇔ x = |
| |
| | (√2 − 2) | | 2 − 4 | |
⇔ x = −3(
√2 − 2) ⇔ x = 6 − 3
√2
17 lut 14:04
J: Ma być: x ≤ 6 − 3√2
17 lut 14:05
alexander: a jak to zaznaczyć na osi x

?
17 lut 14:06
J: Żle .. x ≤ −3(√2 + 2) ⇔ x ≤ −3√2 − 6
17 lut 14:07
J:
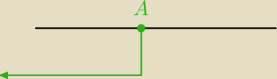
A = −3
√2 − 6
17 lut 14:10
alexander: a możesz napisać rozwiązanie

17 lut 14:11
pigor: ..., lub np. tak :
x√2 ≥ 2x+6 ⇔ −6 ≥ 2x−x√2 ⇔ x(2−√2) ≤ −6 /*(2+√2) >0 ⇔
⇔ x(22−√22) ≤ −6(2+√2) ⇔ x(4−2) ≤ −6(2+√2 /:2 ⇔ x ≤−3(2+√2 ⇔
⇔ x∊(−∞; −3(2+√2)> − szukany zbiór rozwiązań danej nierówności.
17 lut 14:12
 nie jestem pewny na 100%
nie jestem pewny na 100%
 ?
?
 A = −3√2 − 6
A = −3√2 − 6
