PLIS
SZYMON94: w ostrosłupie prawidłowym trójkątnym wysokośc sciany bocznej ma długość 6 a pole sciany bocznej
wynosi 12 pierwiastków z 3 oblicz objetosc i pole powierzchni całkowitej tego ostrosłupa
.BARDZO PROSZE O ROZWIAZANIE CAŁOSCI WRAZ Z RYSUNKIEM DZIEKUJE BARDZO
17 lut 13:45
J: Znając pole powierzchni ściany bocznej i jej wysokość potrafisz obliczyć długość jej podstawy ?
17 lut 13:51
SZYMON94: tak
17 lut 13:56
J: Co jest w podstawie tego ostrosłupa ?
17 lut 13:57
Patronus:
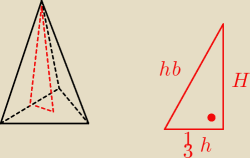
wysokość ściany bocznej ma 6 a pole ściany bocznej ma 12
√3 czyli podstawa ściany bocznej
ma... ?
a = 4
√3
Czyli podstawa tego ostrosłupa ma pole
I została nam wysokość.
Można ją obliczyć z czerwonego trójkąta − to jest trójkąt prostokątny o przyprostokątnej
| | 1 | |
równej wysokości ostrosłupa i drugiej równej |
| wysokości w podstawy oraz |
| | 3 | |
przeciwprostokątnej która jest wysokością ściany bocznej.
| 1 | | 1 | | 4√3*√3 | |
| h = |
| * |
| = 2 |
| 3 | | 3 | | 2 | |
h
b = 6
Czyli H
2 = 2
2 + 6
2
H = 2
√10
Zatem objetość:
V = P
p*H = 12
√3*2
√10 = 24
√30
Chyba że gdzieś sie pomyliłem za co z góry przepraszam

17 lut 13:59
dero2005:
Czyli H
2 = 6
2 − 2
2 =
√32 = 4
√2
zatem objętość
| | Pp*H | | 12√3*4√2 | |
V = |
| = |
| = 16√6 |
| | 3 | | 3 | |
P
c = P
p + 3P
s = 12
√3 + 3*12
√3 = 48
√3
17 lut 19:58
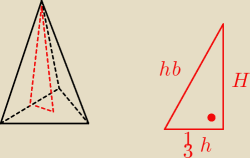 wysokość ściany bocznej ma 6 a pole ściany bocznej ma 12√3 czyli podstawa ściany bocznej
ma... ?
wysokość ściany bocznej ma 6 a pole ściany bocznej ma 12√3 czyli podstawa ściany bocznej
ma... ?
